题目内容
 29、如图,已知在锐角△ABC中,∠ABC=2∠C,∠ABC的平分线与AD垂直于D,求证:AC=2BD.
29、如图,已知在锐角△ABC中,∠ABC=2∠C,∠ABC的平分线与AD垂直于D,求证:AC=2BD.分析:根据题意在BD上截取DF=DE,连接AF,结合题意推出△ADF≌△ADE,即得AE=AF,∠AFD=∠AEF,推出AF=BF,即可推出结论.
解答: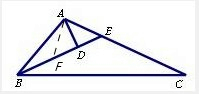 证明:在BD上截取DF=DE,连接AF,
证明:在BD上截取DF=DE,连接AF,
∵DF=DE,AD⊥BF,AD=AD,
∴△ADF≌△ADE,(3分)
∴AE=AF,∠AFD=∠AEF
∵∠ABC=2∠C,BE是∠ABC的平分线,
∴∠ABE=∠C=∠EBC,
∵∠AFE=∠ABE+∠BAF,∠AEF=∠EBC+∠C
∴∠FAB=∠ABF,
∴AF=BF(等角对等边),
∴AC=AE+EC=2BD.(6分)
 证明:在BD上截取DF=DE,连接AF,
证明:在BD上截取DF=DE,连接AF,∵DF=DE,AD⊥BF,AD=AD,
∴△ADF≌△ADE,(3分)
∴AE=AF,∠AFD=∠AEF
∵∠ABC=2∠C,BE是∠ABC的平分线,
∴∠ABE=∠C=∠EBC,
∵∠AFE=∠ABE+∠BAF,∠AEF=∠EBC+∠C
∴∠FAB=∠ABF,
∴AF=BF(等角对等边),
∴AC=AE+EC=2BD.(6分)
点评:本题主要考查等腰三角形的性质、外角的性质、全等三角形的判定和性质,关键在于求证△ADF≌△ADE,∠FAB=∠ABF.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
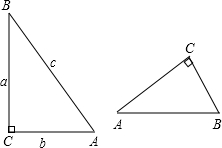 角A的正弦,余弦存在关系式sin2A+cos2A=1试说明.
角A的正弦,余弦存在关系式sin2A+cos2A=1试说明.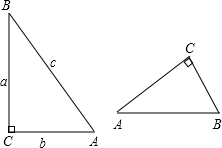 角A的正弦,余弦存在关系式sin2A+cos2A=1试说明.
角A的正弦,余弦存在关系式sin2A+cos2A=1试说明. ,求cosα的值;cosα=
,求cosα的值;cosα=
 如图,已知在锐角△ABC中,∠ABC=2∠C,∠ABC的平分线与AD垂直于D,求证:AC=2BD.
如图,已知在锐角△ABC中,∠ABC=2∠C,∠ABC的平分线与AD垂直于D,求证:AC=2BD. ,求cosα的值;cosα=
,求cosα的值;cosα=
