题目内容
已知一次函数y=kx+b(k、b为常数,且k≠0)的图象(如图1).(1)方程kx+b=0的解为
(2)正比例函数y=mx(m为常数,且m≠0)与一次函数y=kx+b相交于点P(如图2),则不等式组
|
(3)在(2)的条件下,比较mx与kx+b的大小(直接写出结果).

分析:(1)方程kx+b=0的解就是一次函数y=kx+b(k、b为常数,且k≠0)的图象与x轴的交点的横坐标;不等式kx+b<4的解集为,函数图象中纵坐标大于4的部分对应的横坐标的范围;
(2)不等式组
的解集,就是x取同一数值时,两个函数的函数值同时大于0的部分,对应的x的范围;
(3)当所求不等式成立时,一次函数图象对应的点都在反比例图象的上方,根据两个函数的图象可比较mx与kx+b的大小.
(2)不等式组
|
(3)当所求不等式成立时,一次函数图象对应的点都在反比例图象的上方,根据两个函数的图象可比较mx与kx+b的大小.
解答:解:(1)一次函数y=kx+b(k、b为常数,且k≠0)的图象与x轴的交点的横坐标是2,故方程的解是x=2,
一次函数经过点(0,4),故不等式的解集是x>0(4分)
故答案是:x=2和x>0;
(2)0<x<2(6分)
(3)当x<1时,mx<kx+b(7分)
当x=1时,mx=kx+b(8分)
当x>1时,mx>kx+b(9分)
一次函数经过点(0,4),故不等式的解集是x>0(4分)
故答案是:x=2和x>0;
(2)0<x<2(6分)
(3)当x<1时,mx<kx+b(7分)
当x=1时,mx=kx+b(8分)
当x>1时,mx>kx+b(9分)
点评:本题考查了一次函数与不等式(组)的关系及数形结合思想的应用.解决此类问题关键是仔细观察图形,注意几个关键点(交点、原点等),做到数形结合.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
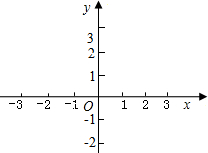 已知一次函数y=kx+2的图象经过A(-1,1).
已知一次函数y=kx+2的图象经过A(-1,1). m≠0)的图象相交于点 A(1,3)、B(n,-1)两点.
m≠0)的图象相交于点 A(1,3)、B(n,-1)两点.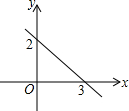 已知一次函数y=kx+b的图象如图所示,指出k、b的符号,并求出k和b的值.
已知一次函数y=kx+b的图象如图所示,指出k、b的符号,并求出k和b的值.