题目内容
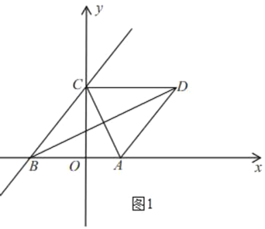
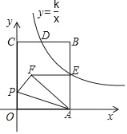
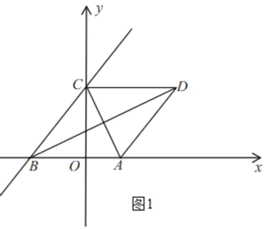
【题目】如图,在平面直角坐标系中,一次函数y=![]() x+4的图象与x轴交于点B,与y轴交于点C,二次函数y=
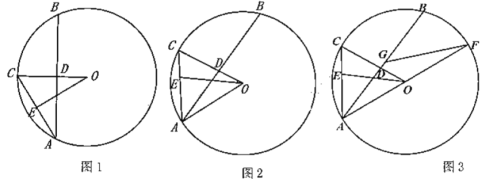
x+4的图象与x轴交于点B,与y轴交于点C,二次函数y=![]() x2+bx+c的图象经过点A(2,0)和点C,抛物线与x轴交于点A和点E(点A在点E的左侧),连接AC,将△ABC沿AC折叠,得到点B的对应点为点D.
x2+bx+c的图象经过点A(2,0)和点C,抛物线与x轴交于点A和点E(点A在点E的左侧),连接AC,将△ABC沿AC折叠,得到点B的对应点为点D.
(1)求二次函数的表达式;
(2)求点D坐标,并判定点D是否在该二次函数的图象上;
(3)①在线段AC上找一点F,使得△OBF的周长最小,直接写出此时点F的坐标.②在①的基础上,过点F的一条直线与抛物线对称轴右侧部分交于点N,交线段AD于点M,连接NA、ND,使△AMF与△AMN的面积比为4:1,请直接写出△AND的面积.
【答案】(1)![]() ;(2)D(5,4),点D是否在该二次函数的图象上;(3)①F
;(2)D(5,4),点D是否在该二次函数的图象上;(3)①F![]() ;②△AND的面积为
;②△AND的面积为![]() .
.
【解析】
(1)先根据一次函数的解析式求出点C坐标,再利用待定系数法即可得;
(2)先根据一次函数的解析式求出点B坐标,再根据点![]() 坐标可得
坐标可得![]() ,再根据旋转的性质、菱形的判定与性质可得CD∥AB,CD=AB=5,从而可得点D坐标,然后根据二次函数的解析式即可得出答案;
,再根据旋转的性质、菱形的判定与性质可得CD∥AB,CD=AB=5,从而可得点D坐标,然后根据二次函数的解析式即可得出答案;
(3)①先由题(2)的结论得出点B、D关于AC对称,再根据轴对称的性质、两点之间线段最短得出,![]() 的周长最小时,点F的位置,然后利用待定系数法求出AC、OD的解析式,联立求解即可得点F坐标;
的周长最小时,点F的位置,然后利用待定系数法求出AC、OD的解析式,联立求解即可得点F坐标;
②先根据“△AMF与△AMN的面积比为4:1”求出FM=4MN,再利用待定系数法求出AD的解析式,从而可得![]() 的长,然后根据相似三角形的判定与性质可得NH的长,最后利用点A、D坐标和三角形的面积公式即可得.
的长,然后根据相似三角形的判定与性质可得NH的长,最后利用点A、D坐标和三角形的面积公式即可得.
(1)∵一次函数![]() 的图象与y轴交于点C
的图象与y轴交于点C
∴![]()
∵点![]() 在二次函数
在二次函数![]() 的图象上
的图象上
∴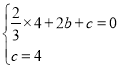 ,解得
,解得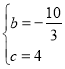
故二次函数的解析式为![]() ;
;
(2)如图1,对于一次函数![]()
令y=0,则![]()
∴![]()
∴![]()
∵![]()
∴![]()
∴BC=AB
由折叠的性质可知,BC=CD,AB=AD
∴AB=AD=CD=BC
∴四边形ABCD是菱形
∴CD∥AB,CD=AB=5
∴点D横坐标为5,纵坐标与点C纵坐标相等
![]()
由(1)知,二次函数的解析式为![]()
当x=5时,![]()
∴点D在二次函数![]() 的图象上
的图象上
故点D坐标为![]() ,且在二次函数
,且在二次函数![]() 的图象上;
的图象上;
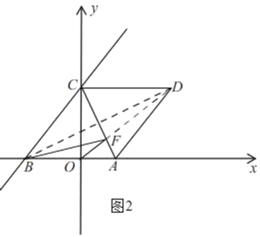
(3)①如图2,连接FD、BD
由(2)知,四边形ABCD是菱形
∴点B关于AC的对称点为D
![]()
![]() 的周长为
的周长为![]()
由两点之间线段最短得,当点![]() 在一条线上时,
在一条线上时,![]() 的周长最小
的周长最小
![]()
∴直线OD的解析式为![]()
![]()
∴直线AC的解析式为![]()
联立OD、AC的函数解析式得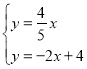
解得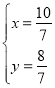
∴![]() ;
;
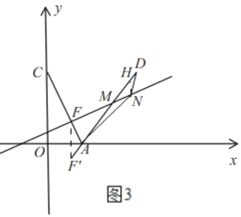
②如图3,由①知,![]()
∵△AMF与△AMN的面积比为![]()
∴FM=4MN
∵![]()
∴直线AD的解析式为![]()
过点F作![]() 轴,交DA的延长线于点
轴,交DA的延长线于点![]()
将![]() 代入
代入![]() 得,
得,![]()
∴![]()
![]()
过点N作NH∥y轴,交AD于H
∴![]()
∴![]()
∴![]()
∴![]()
设点A横坐标为![]() ,点D横坐标为
,点D横坐标为![]()
∴![]()
故△AND的面积为![]() .
.