Question

【题目】如图，在菱形 中， ， ， 是 的中点．过点 作 ，垂足为 ．将 沿点 到点 的方向平移，得到 ．设 、 分别是 、 的中点，当点 与点 重合时，四边形 的面积为（ ）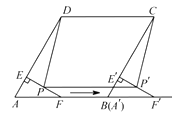

A.
B.
C.
D.

Answer 1

【答案】A
【解析】解：过点E作EI⊥AB，过P作PH⊥AB于H，连结DF，则DF⊥AB，
由平移的性质可得PP′=AB，PP′//AB，又∵在菱形ABCD中，AB//CD，
AB=CD，∴PP′//CD，PP′=CD，∴四边形CDPP′是平行四边形，
已知菱形的边长为8，∠A=60°，则DF=8×sin60°=4
F为AB的中点，则AF=8÷2=4；已知∠A=60°，EF⊥AD，则∠AFE=30°，则AE=2
EI=AE×sin60°=2×=，
P是EF的中点，且易知道PH//EI，所以PH=÷2=
SPP′CD=8×（4-）=28
故选A.

【考点精析】通过灵活运用平行四边形的判定与性质和特殊角的三角函数值，掌握若一直线过平行四边形两对角线的交点，则这条直线被一组对边截下的线段以对角线的交点为中点，并且这两条直线二等分此平行四边形的面积；分母口诀：30度、45度、60度的正弦值、余弦值的分母都是2，30度、45度、60度的正切值、余切值的分母都是3，分子口诀：“123，321，三九二十七”即可以解答此题．