Question

已知，K是图中所示正方体中棱CD的中点，连接KE、AE，则cos∠KEA的值为________．

Answer 1

分析：设正方体的棱长为a．先根据正方体的性质，由勾股定理，分别计算出AE、AK、EK的长度，得出△AKE为等腰三角形，再过点K作KM⊥AE于M，根据等腰三角形三线合一的性质得出EM=AE，∠KME=90°，然后在直角三角形KEM中根据余弦函数的定义进行解答即可．
解答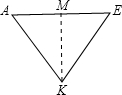：解：连接AK．设正方体的棱长为a．
由勾股定理，得AE=a，AK=EK=a．
过点K作KM⊥AE于M，则AM=EM=AE=a．
在直角三角形KEM中，∠KME=90°，
∴cos∠KEA====．
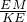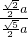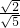故答案为．
点评：本题考查了正方体的性质，勾股定理，等腰三角形的性质及解直角三角形，综合性较强，难度一般．