题目内容
已知在三角形ABC中，AD是BC上的中线，求证：S△ABD=S△ACD=| 1 |
| 2 |
考点：三角形的面积
专题：证明题
分析：根据等底等高的两个三角形面积相等知，三角形的中线把三角形的面积分为相等的两部分，所以S△ABD=S△ACD．
解答：解：根据等底同高可得：S△ABD=S△ACD．
因为S△ABC=S△ABD+S△ACD，
所以S△ABD=S△ACD=
S△ABC．
因为S△ABC=S△ABD+S△ACD，
所以S△ABD=S△ACD=
| 1 |
| 2 |
点评：本题考查了三角形中线的性质，等底等高的两个三角形面积相等．
练习册系列答案
相关题目
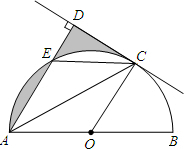如图，AB是⊙O的直径，C是半圆O上的一点，AC平分∠DAB，AD⊥CD，垂足为D，AD交⊙O于E，连接CE．
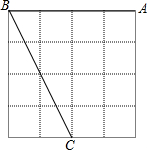如图所示，每个小正方形的边长为1
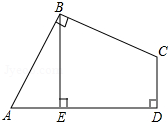如图，在四边形ABCD中，AB=BC，∠ABC=∠CDA=90°，BE⊥AD，垂足为E．|-
|=（ ）
| 2 |
| 11 |
A、
| ||
B、-
| ||
C、
| ||
D、-
|