Question

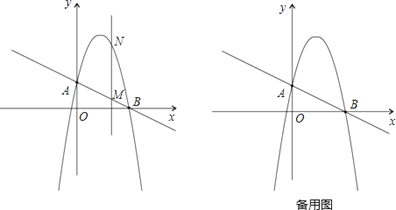
【题目】已知抛物线y=ax2+bx+c的图象如图所示，根据图象解答下列问题：

（1）抛物线与x轴的另一个交点坐标：　　　　 ；

（2）不等式ax2+bx+c＜0的解是　　　　 ；

（3）方程ax2+bx+c=-3的两个根是　　　　 ；

（4）y随x的增大而减小的自变量x的取值范围是　　　　 ；

（5）求出抛物线的解析式及顶点坐标．

Answer 1

【答案】（1）（3，0）；（2）1＜x＜3；（3）x=0或x=2；（4）x＜1；（5）y=x22x3，顶点坐标为（1，4）．

【解析】

（1）根据抛物线的对称性求解；

（2）根据图像在x轴下方时，x的取值范围即为不等式的解；

（3）将方程变为ax2+bx+c+3=0，由二次函数y= ax2+bx+c+3向上平移3个单位后，与x轴的交点坐标，可得出方程的解.

（4）根据抛物线的增减性可判断x的取值范围；

（5）设抛物线解析式为，代入（0，-3）即可得抛物线解析式，再用配方法改写为顶点式，即可得顶点坐标.

（1）依题意得抛物线的对称轴为x=1，与x轴的一个交点坐标为（1，0），

∴抛物线与x轴的另一个交点坐标为（3，0）；

（2）∵抛物线与x轴的两个交点坐标为（3，0）,（1，0），

∴不等式ax2+bx+c＜0的解是1＜x＜3；

（3）将方程变为ax2+bx+c+3=0，,二次函数y= ax2+bx+c+3向上平移3个单位后，与x轴交于原点和（2,0），∴方程ax2+bx+c=-3的两个根是x=0或x=2；

（4）∵抛物线开口向上，对称轴为x=1

∴y随x的增大而减小的自变量x的取值范围是x＜1；

（5）设抛物线解析式为，代入（0，-3）得

，解得

∴，

∴顶点坐标为（1，4）．