题目内容
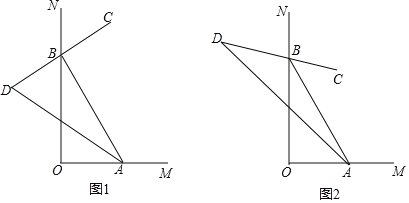
【题目】如图,∠MON=ɑ(0°<ɑ<180°),点A.B分别在OM、ON上运动(不与点O重合).
(1)如图1,∠MON=90°,BC是∠ABN的平分线,BC的反方向延长线与∠BAO的平分线交与点D.
①若∠BAO=60°,则∠D=___.
②猜想:∠D的度数是否随A,B的移动发生变化?并说明理由。
(2)如图2,∠MON=α(0°<α<180°)”,∠ABC=![]() ∠ABN,∠BAD=
∠ABN,∠BAD=![]() ∠BAO,其余条件不变,则∠D=___°(用含α、n的代数式表示)
∠BAO,其余条件不变,则∠D=___°(用含α、n的代数式表示)
【答案】①45;②∠D的度数不随A,B的移动发生变化; ![]()
【解析】
(1)①根据邻补角的定义及角平分线定义求出∠BAD =30°,∠ABC =75°,然后根据三角形外角的性质可求出∠D;②设∠BAO=x,步骤同①可得∠D的度数不随A,B的移动发生变化;
(2)根据三角形外角的性质可得∠D=∠ABC-∠BAD,然后将∠ABC=![]() ∠ABN,∠BAD=
∠ABN,∠BAD=![]() ∠BAO代入化简,即可得出结果.
∠BAO代入化简,即可得出结果.
解:(1)①∵∠MON=90°,∠BAO=60°,
∴∠ABO=30°,∠BAD=![]() ∠BAO =30°
∠BAO =30°
∴∠ABN=150°,
∴∠ABC=![]() ∠ABN=75°,
∠ABN=75°,
∴∠D=∠ABC-∠BAD=45°;
②∠D的度数不随A,B的移动发生变化;
理由:设∠BAO=x,
∴∠ABO=90°-x,∠BAD=![]() ∠BAO=
∠BAO=![]() ,
,
∴∠ABN=180°-(90°-x)=90°+x,
∴∠ABC=![]() ∠ABN=45°+
∠ABN=45°+![]() ,
,
∴∠D=∠ABC-∠BAD=45°+![]() -
-![]() =45°,
=45°,
∴∠D的度数不随A,B的移动发生变化;
(2)∵∠MON=α,∠ABC=![]() ∠ABN,∠BAD=
∠ABN,∠BAD=![]() ∠BAO,
∠BAO,
∴∠D=∠ABC-∠BAD=![]() ∠ABN-
∠ABN-![]() ∠BAO=
∠BAO=![]() (∠ABN-∠BAO)=
(∠ABN-∠BAO)=![]() ∠MON=
∠MON=![]() .
.

练习册系列答案
 新思维假期作业寒假吉林大学出版社系列答案
新思维假期作业寒假吉林大学出版社系列答案
相关题目