题目内容
如图，在⊙O中，CD是直径，AB是弦，AB⊥CD于M，CD=10cm，DM：CM=1：4，求弦AB的长．分析：连接OA，先由CD=10cm，DM：CM=1：4求出CM、DM及OA的长，再由垂径定理得出AB=2AM，由勾股定理求出AM的长，进而可得出结论．
解答：
解：如图，连接OA．
∵CD=10cm，DM：CM=1：4，
∴CM=8，DM=2，
∴OM=5-2=3cm，OA=5cm，
又∵CD是直径，AB是弦，AB⊥CD于M，
∴AB=2AM．…（3分）
在Rt△AOM中，
∵AM=
=
=4cm，
∴AB=8cm．
解：如图，连接OA．∵CD=10cm，DM：CM=1：4，
∴CM=8，DM=2，
∴OM=5-2=3cm，OA=5cm，
又∵CD是直径，AB是弦，AB⊥CD于M，
∴AB=2AM．…（3分）
在Rt△AOM中，
∵AM=
| OA2-OM2 |
| 52-32 |
∴AB=8cm．
点评：本题考查的是垂径定理及勾股定理，根据题意作出辅助线，构造出直角三角形是解答此题的关键．
练习册系列答案
相关题目
13、如图，在△ABC中，CD是AB边上的中线，线段AC比BC短2cm，则△BCD和△ACD的周长的差是
14、如图，在△ABC中，CD平分∠ACB，DE∥AC，DC∥EF，则与∠ACD相等角有
如图，在△ABC中，CD、BE分别是AB、AC边上的高，∠EBC=45°，BE=6，CD=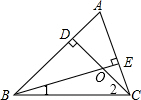
如图，在△ABC中，CD是AB边上的高，BE是AC边上的高，点O是两条高线的交点，则∠A与∠1+∠2的关系是（ ）
如图，在⊙O中，