题目内容
在方程组
中，若未知数x、y满足x+y＞0，则m的取值范围是________．
m＜3
分析：将方程组中两方程相加，便可得到关于x+y的方程，再根据x+y＞0，即可求出m的取值范围．
解答：（1）+（2）得，（2x+y）+（x+2y）=（1-m）+2，
即3x+3y=3-m，
可得x+y=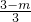
，
∵x+y＞0，即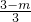＞0，故m＜3．
点评：此题考查的是二元一次方程组和不等式的性质，要注意x+y＞0，则解出x，y关于m的式子，最终求出m的取值范围．
分析：将方程组中两方程相加，便可得到关于x+y的方程，再根据x+y＞0，即可求出m的取值范围．
解答：（1）+（2）得，（2x+y）+（x+2y）=（1-m）+2，
即3x+3y=3-m，
可得x+y=
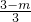，∵x+y＞0，即
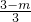＞0，故m＜3．点评：此题考查的是二元一次方程组和不等式的性质，要注意x+y＞0，则解出x，y关于m的式子，最终求出m的取值范围．
练习册系列答案
课时训练江苏人民出版社系列答案
黄冈经典趣味课堂系列答案
启东小题作业本系列答案
相关题目
中，若未知数x、y满足x+y＞0，则m的取值范围是 .
中，若未知数x、y满足x+y＞0，则m的取值范围是 .
中，若未知数x 、y满足 x＋y>0，则m的取值范围是
．
中，若未知数x、y满足x+y＞0，则m的取值范围是 .在方程组
中，若未知数x，y满足x+y＞0，则m的取值范围在数轴上的表示应是如图所示的（ ）
|
| A． |
| B． |
| C． |
| D． |
|
