Question

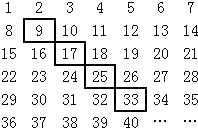
把2012个正整数1，2，3，4，…，2012按如图方式排列成一个表．
（1）用如图方式框住表中任意4个数，记左上角的一个数为x，则另三个数用含x的式子表示出来，从小到大依次是

x+8

，

x+16

，

x+24

．
（2）由（1）中能否框住这样的4个数，它们的和会等于244吗？若能，则求出x的值；若不能，则说明理由．

Answer 1

分析：（1）表中数字有一定规律，上下相差7的倍数，左右相差1，利用规律列方程即可解答．
（2）表示出四个数，列出方程解得x即可，要注意和实际相结合，不能盲目求解．

解答：解：（1）∵记左上角的一个数为x，
∴另三个数用含x的式子表示为：x+8，x+16，x+24．
故答案为：x+8，x+16，x+24；

（2）不能．
设：x+（x+8）+（x+16）+（x+24）=244，
解得：x=49．
∵49是第七行最后一个数，
∴不可以用如图方式框住．

点评：本题主要考查对一元一次方程的应用，要把实际问题抽象到解方程中来是解题关键．