题目内容
 △DAC和△EBC均是等边三角形,连AE、BD,△ACE与△BCD全等吗?请说明理由.
△DAC和△EBC均是等边三角形,连AE、BD,△ACE与△BCD全等吗?请说明理由.分析:欲证三角形全等,利用全等的条件进行判定即可;因为△DAC和△ECB均为等边三角形,即有∠ACD=∠ECB=60°,即∠ACD+∠DCE=∠ECB+∠DCE,即可得出∠ACE=∠DCB,再利用边的关系,即可得证△ACE≌△DCB(SAS).
解答:解:△ACE≌△DCB;
理由:∵∠ACD=∠ECB=60°,
∴∠ACD+∠DCE=∠ECB+∠DCE,
∴∠ACE=∠DCB,
∵在△ACE和△DCB中
,
∴△ACE≌△DCB(SAS).
理由:∵∠ACD=∠ECB=60°,
∴∠ACD+∠DCE=∠ECB+∠DCE,
∴∠ACE=∠DCB,
∵在△ACE和△DCB中
|
∴△ACE≌△DCB(SAS).
点评:本题主要考查了等边三角形的性质和全等三角形的判定和性质,属于中等题目,要求学生具备一定的几何知识和解题能力.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 8、如图,△DAC和△EBC均是等边三角形,AE、BD分别与CD、CE交于点M、N,有如下结论:①△ACE≌△DCB; ②CM=CN;③AC=DN.其中,正确结论的个数是( )
8、如图,△DAC和△EBC均是等边三角形,AE、BD分别与CD、CE交于点M、N,有如下结论:①△ACE≌△DCB; ②CM=CN;③AC=DN.其中,正确结论的个数是( ) 如图,△DAC和△EBC均是等边三角形,AE、BD分别与CD、CE交于点M、N,有如下结论:①△ACE≌△DCB;②CM=CN;③AC=DN.其中,结论正确的有
如图,△DAC和△EBC均是等边三角形,AE、BD分别与CD、CE交于点M、N,有如下结论:①△ACE≌△DCB;②CM=CN;③AC=DN.其中,结论正确的有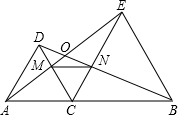 如图,点A、C、B在同一直线上,△DAC和△EBC均是等边三角形,AE与BD交于点O,AE、BD分别与CD、CE交于点M、N,有如下结论:①AE=BD;②△ACM≌△DCN;③EM=BN;④MN∥BC;⑤∠DOA=60°,其中,正确的结论个数是( )
如图,点A、C、B在同一直线上,△DAC和△EBC均是等边三角形,AE与BD交于点O,AE、BD分别与CD、CE交于点M、N,有如下结论:①AE=BD;②△ACM≌△DCN;③EM=BN;④MN∥BC;⑤∠DOA=60°,其中,正确的结论个数是( )