题目内容
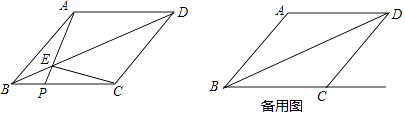
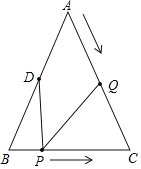
【题目】如图,已知![]() 中,
中,![]() ,
,![]() ,点D为AB的中点,如果点P在线段BC上以
,点D为AB的中点,如果点P在线段BC上以![]() 的速度由点B向点C运动,同时,点Q在线段AC上由点A向点C以
的速度由点B向点C运动,同时,点Q在线段AC上由点A向点C以![]() 的速度运动
的速度运动![]() 若点P、Q两点分别从点B、A同时出发.
若点P、Q两点分别从点B、A同时出发.
![]() 经过2秒后,求证:
经过2秒后,求证:![]() ≌
≌![]()
![]() 若
若![]() 的周长为18cm,问经过几秒钟后,
的周长为18cm,问经过几秒钟后,![]() 为等腰三角形?
为等腰三角形?
【答案】![]() 经过1秒或
经过1秒或![]() 秒或
秒或![]() 秒时,
秒时,![]() 是等腰三角形.
是等腰三角形.
【解析】
![]() 经过2秒后,
经过2秒后,![]() ,则
,则![]() ,
,![]() ,结合已知可得
,结合已知可得![]() ,
,![]() ,
,![]() ,即可根据SAS可证得
,即可根据SAS可证得![]() ≌
≌![]() .
.![]() 由
由![]() ≌
≌![]() 可得
可得![]() ,再根据三角形的外角即可得证.
,再根据三角形的外角即可得证.
![]() 可设点Q的运动时间为
可设点Q的运动时间为![]() 是等腰三角形,则可知
是等腰三角形,则可知![]() ,
,![]() ,
,![]() ,
,![]() ,再根据
,再根据![]() 的周长为18cm,得出
的周长为18cm,得出![]() ,当
,当![]() 为等腰三角形时,分三种情况从而求得t的值即可.
为等腰三角形时,分三种情况从而求得t的值即可.
解:![]()
![]() 当P,Q两点分别从B,A两点同时出发运动2秒时,
当P,Q两点分别从B,A两点同时出发运动2秒时,
有![]() ,
,![]() ,
,
则![]() ,
,
![]() ,
,
![]() 是AB的中点,
是AB的中点,
![]() ,
,
![]() ,
,![]() ,
,
又![]() 中,
中,![]() ,
,
![]() ,
,
在![]() 和
和![]() 中,
中,
 ,
,
![]() ≌
≌![]()
![]() ≌
≌![]()
![]()
![]()
![]() 设当P,Q两点同时出发运动t秒时,
设当P,Q两点同时出发运动t秒时,
有![]() ,
,![]()
![]() 的取值范围为
的取值范围为![]() ,
,
则![]() ,
,![]() ,
,
![]() 的周长为18cm,
的周长为18cm,
![]()
![]() ,
,
要使![]() 是等腰三角形,则可分为三种情况讨论:
是等腰三角形,则可分为三种情况讨论:
![]() 当
当![]() 时,则有
时,则有![]()
解得:![]()
![]() 当
当![]() 时,则有
时,则有![]()
解得:![]()
![]() 当
当![]() 时,则有
时,则有![]()
解得:![]()
三种情况均符合t的取值范围.
综上所述,经过1秒或![]() 秒或
秒或![]() 秒时,
秒时,![]() 是等腰三角形.
是等腰三角形.

练习册系列答案
相关题目