题目内容
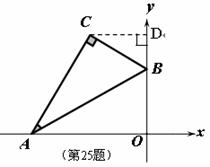
如图,平面直角坐标系中,将含30°的三角尺的直角顶点C落在第二象限。其斜边两端点A、B分别落在x轴、y轴上,且AB=12cm
(1) 若OB=6cm.
① 求点C的坐标;
② 若点A向右滑动的距离与点B向上滑动的距离相等,求滑动的距离;
(2) 点C与点O的距离的最大值= cm.

解:(1)① 过点C作y轴的垂线,垂足为D,
在Rt△AOB中,AB=12, OB=6,则BC=6,
∴∠BAO=30°,∠ABO=60°,
又∠CBA=60°,∴∠CBD=60°,∠BCD=30°,
∴BD=3,CD=3 .
.
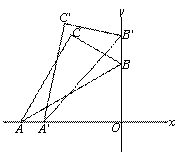
② 设点A向右滑动的距离为x,根据题意得点B向动的距离也为x,
AO=12×cos∠BAO=12×cos30°=6 .
.
 ∴A'O=6
∴A'O=6 -x,B'O=6+x ,A'B'=AB=12
-x,B'O=6+x ,A'B'=AB=12
在△A'O B'中,由勾股定理得,
(6 -x)²+(6+x)²=12²
-x)²+(6+x)²=12²
解得,x=6( -1)
-1)
∴滑动的距离为6( -1).
-1).
(2)设点 C的坐标为(x,y),过C作CE ⊥ x轴,CD ⊥ y轴, 垂足分别为E,D
C的坐标为(x,y),过C作CE ⊥ x轴,CD ⊥ y轴, 垂足分别为E,D
则OE=-x,OD=y,
 ∵∠ACE+∠BCE=90°,∠DCB+∠BCE=90°
∵∠ACE+∠BCE=90°,∠DCB+∠BCE=90°
∴∠ACE=∠DCB,
又∵∠AEC=∠BDC=90°,
∴△ACE ∽ △BCD
∴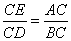 ,即
,即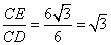 ,
,
 ∴y=-
∴y=- x,
x,
OC²=x²+y²= x²+(- x)²=4x²,
x)²=4x²,
∴当︱x︱取最大值时即C到y轴距离最大时OC²有最
大 值,即OC取最大值,如图,即当C'B'转到与y轴垂时
值,即OC取最大值,如图,即当C'B'转到与y轴垂时
.此时OC=12.

练习册系列答案
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案
相关题目
 ,为美化校园环境,某校计划在一块长为60米,宽为4米的长方形空地上修建一个长方形花圃,并将花圃四周余下的空地修建成同样宽的通道,设通道宽为
,为美化校园环境,某校计划在一块长为60米,宽为4米的长方形空地上修建一个长方形花圃,并将花圃四周余下的空地修建成同样宽的通道,设通道宽为 米.
米. )如果通道所占面积是整个长方形空地面积的
)如果通道所占面积是整个长方形空地面积的 ,求出此时通道的宽.
,求出此时通道的宽. (元)、
(元)、 (元)与修建面积
(元)与修建面积 之间的函数关系如图13-2所示,如果学校决定由该公司承建此项目,并要
之间的函数关系如图13-2所示,如果学校决定由该公司承建此项目,并要



 B.
B.
 D.
D.
 C D.∠C=∠EDF
C D.∠C=∠EDF
 的绝对值是
的绝对值是 . (B)
. (B)  2.
2. 时,代数式
时,代数式 的值相等,则
的值相等,则 时,代数式
时,代数式