题目内容
如图1,抛物线y=x2+x-4与y轴交于点A,E(0,b)为y轴上一动点,过点E的直线y=x+b与抛物线交于点B、C.
(1)求点A的坐标;
(2)当b=0时(如图2),求△ABE与△ACE的面积.
(3)当b>-4时,△ABE与△ACE的面积大小关系如何?为什么?
(4)是否存在这样的b,使得△BOC是以BC为斜边的直角三角形?若存在,求出b;若不存在,说明理由.
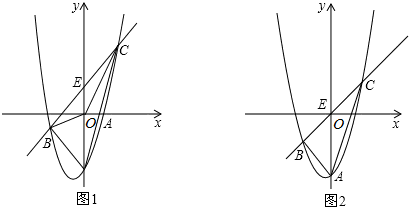
解:(1)将x=0,代入抛物线的解析式得:y=-4,
得点A的坐标为(0,-4),
答:点A的坐标为(0,-4).
(2)当b=0时,直线为y=x,
由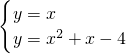 ,
,
解得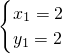 ,
,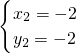 ,
,
∴B、C的坐标分别为B(-2,-2),C(2,2),
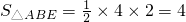 ,
, ,
,
答:△ABE的面积是4,△ACE的面积是4.
(3)当b>-4时,S△ABE=S△ACE,
理由是:由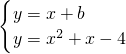 ,
,
解得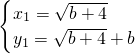 ,
, ,
,
∴B、C的坐标分别为:
B(-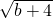 ,-
,-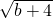 +b),C(
+b),C(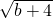 ,
,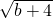 +b),
+b),
作BF⊥y轴,CG⊥y轴,垂足分别为F、G,
则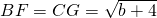 ,
,
而△ABE和△ACE是同底的两个三角形,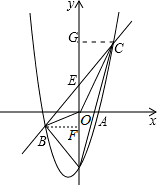
∴S△ABE=S△ACE.
答:当b>-4时,△ABE与△ACE的面积大小关系是相等.
(4)存在这样的b,
∵BF=CG,∠BEF=∠CEG,∠BFE=∠CGE=90°,
∴△BEF≌△CEG,
∴BE=CE,
即E为BC的中点,
所以当OE=CE时,△OBC为直角三角形,
∵B(-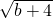 ,-
,-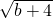 +b),E(0,b),
+b),E(0,b),
∴GE=EF=|-(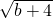 +b)+b|=
+b)+b|=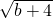 =CG
=CG
GE=GC=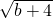 ,
,
∴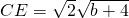 ,而OE=|b|,
,而OE=|b|,
∴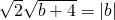 ,
,
解得b1=4,b2=-2,
∴当b=4或-2时,△OBC为直角三角形,
答:存在这样的b,使得△BOC是以BC为斜边的直角三角形,b的值是4或-2.
分析:(1)将x=0,代入抛物线的解析式即可;
(2)当b=0时,直线为y=x,解由y=x和y=x2+x-4组成的方程组即可求出B、C的坐标,再利用三角形的面积公式即可求出面积;
(3)当b>-4时,△ABE与△ACE的面积相等,理由是解由直线和抛物线组成的方程组,即可求出交点的坐标,作BF⊥y轴,CG⊥y轴,垂足分别为F、G,根据点的坐标得到△ABE和△ACE是同底的两个三角形,即可得出答案;
(4)存在这样的b,根据全等三角形的判定证△BEF≌△CEG,推出BE=CE,根据直角三角形的性质,当OE=CE时,△OBC为直角三角形,代入即可求出b的值.
点评:本题主要考查对二次函数图象上点的坐标特征,解二元一次方程组,三角形的面积,全等三角形的性质和判定,直角三角形的性质等知识点的理解和掌握,熟练地运用这些性质进行计算是解此题的关键,题型较好,综合性强.
得点A的坐标为(0,-4),
答:点A的坐标为(0,-4).
(2)当b=0时,直线为y=x,
由
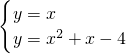 ,
,解得
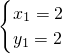 ,
,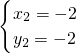 ,
,∴B、C的坐标分别为B(-2,-2),C(2,2),
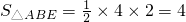 ,
, ,
,答:△ABE的面积是4,△ACE的面积是4.
(3)当b>-4时,S△ABE=S△ACE,
理由是:由
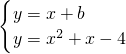 ,
,解得
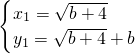 ,
, ,
,∴B、C的坐标分别为:
B(-
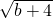 ,-
,-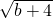 +b),C(
+b),C(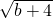 ,
,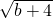 +b),
+b),作BF⊥y轴,CG⊥y轴,垂足分别为F、G,
则
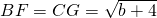 ,
,而△ABE和△ACE是同底的两个三角形,

∴S△ABE=S△ACE.
答:当b>-4时,△ABE与△ACE的面积大小关系是相等.
(4)存在这样的b,
∵BF=CG,∠BEF=∠CEG,∠BFE=∠CGE=90°,
∴△BEF≌△CEG,
∴BE=CE,
即E为BC的中点,
所以当OE=CE时,△OBC为直角三角形,
∵B(-
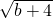 ,-
,-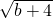 +b),E(0,b),
+b),E(0,b),∴GE=EF=|-(
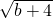 +b)+b|=
+b)+b|=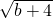 =CG
=CGGE=GC=
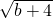 ,
,∴
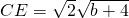 ,而OE=|b|,
,而OE=|b|,∴
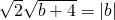 ,
,解得b1=4,b2=-2,
∴当b=4或-2时,△OBC为直角三角形,
答:存在这样的b,使得△BOC是以BC为斜边的直角三角形,b的值是4或-2.
分析:(1)将x=0,代入抛物线的解析式即可;
(2)当b=0时,直线为y=x,解由y=x和y=x2+x-4组成的方程组即可求出B、C的坐标,再利用三角形的面积公式即可求出面积;
(3)当b>-4时,△ABE与△ACE的面积相等,理由是解由直线和抛物线组成的方程组,即可求出交点的坐标,作BF⊥y轴,CG⊥y轴,垂足分别为F、G,根据点的坐标得到△ABE和△ACE是同底的两个三角形,即可得出答案;
(4)存在这样的b,根据全等三角形的判定证△BEF≌△CEG,推出BE=CE,根据直角三角形的性质,当OE=CE时,△OBC为直角三角形,代入即可求出b的值.
点评:本题主要考查对二次函数图象上点的坐标特征,解二元一次方程组,三角形的面积,全等三角形的性质和判定,直角三角形的性质等知识点的理解和掌握,熟练地运用这些性质进行计算是解此题的关键,题型较好,综合性强.

练习册系列答案
 金版课堂课时训练系列答案
金版课堂课时训练系列答案 单元全能练考卷系列答案
单元全能练考卷系列答案 新黄冈兵法密卷系列答案
新黄冈兵法密卷系列答案
相关题目
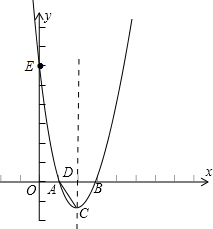 已知二次函数的图象是经过点A(1,0),B(3,0),E(0,6)三点的一条抛物线.
已知二次函数的图象是经过点A(1,0),B(3,0),E(0,6)三点的一条抛物线. 阅读材料:如图1,过△ABC的三个顶点分别作出与水平线垂直的三条直线,外侧两条直线之间的距离叫△ABC的“水平宽”(a),中间的这条直线在△ABC内部线段的长度叫△ABC的“铅垂高”(h).我们可得出一种计算三角形面积的新方法:S△ABC=
阅读材料:如图1,过△ABC的三个顶点分别作出与水平线垂直的三条直线,外侧两条直线之间的距离叫△ABC的“水平宽”(a),中间的这条直线在△ABC内部线段的长度叫△ABC的“铅垂高”(h).我们可得出一种计算三角形面积的新方法:S△ABC=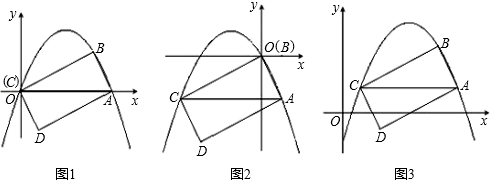
 如图,将抛物线
如图,将抛物线