题目内容
已知:如图,AB是半圆O的直径,C是半圆上一点,连接AC、BC、过O点作AB的垂线,交BC于E,交半 圆于F,交AC的延长线于D.
圆于F,交AC的延长线于D.(1)求证:
| S△OEC |
| S△OCD |
| EC2 |
| CD2 |
(2)如果OA=2,点C在弧AF上运动(不与点A,F重合).设OE的长为x,△AOD的面积为y,求y和x之间的函数关系式,写出自变量x的取值范围,并画出函数图象.
分析:(1)由AB是直径得出∠ACB是直角,推出∠A和∠B的和为90°,再由OD与AB垂直得出∠A与∠D的和为90°,从而得出角的等量关系,即可得到△OEC∽△OCD,从而推出结论.
(2)由△OEC∽△OCD得出边的比例关系,再由三角形的面积公式即可得出y和x之间的函数关系式,再求出自变量x的取值范围即可.
(2)由△OEC∽△OCD得出边的比例关系,再由三角形的面积公式即可得出y和x之间的函数关系式,再求出自变量x的取值范围即可.
解答:(1)证明:∵OC=OB
∴∠OCB=∠B
∵AB是⊙O的直径
∴∠ACB=90°
∴∠A+∠B=90°
∵OD⊥AB
∴∠A+∠D=90°
∴∠D=∠B=∠OCB
∵∠EOC=∠COD
∴△OEC∽△OCD
∴
=(
)2
∴
=
(6分)
(2)解:∵△OEC∽△OCD
∴
=
∴OC2=OE•OD
∵OC=2,OE=x
∴22=x•OD
∴OD=
(8分)
又∵y=
×AO•OD,∴y=
×2×
,
∴y=
(9分)
∴自变量x的取值范围是0<x<2(10分)
∴∠OCB=∠B
∵AB是⊙O的直径
∴∠ACB=90°
∴∠A+∠B=90°
∵OD⊥AB
∴∠A+∠D=90°
∴∠D=∠B=∠OCB
∵∠EOC=∠COD
∴△OEC∽△OCD
∴
| SOEC |
| SOCD |
| EC |
| CD |
∴
| SOEC |
| SOCD |
| EC2 |
| CD2 |
(2)解:∵△OEC∽△OCD
∴
| OC |
| OE |
| OD |
| OC |
∴OC2=OE•OD
∵OC=2,OE=x
∴22=x•OD
∴OD=
| 4 |
| x |
又∵y=
| 1 |
| 2 |
| 1 |
| 2 |
| 4 |
| x |
∴y=
| 4 |
| x |
∴自变量x的取值范围是0<x<2(10分)
点评:本题主要考查了相似三角形的判定和性质,以及二元一次函数的应用,综合性强,难度适中.

练习册系列答案
 时刻准备着暑假作业原子能出版社系列答案
时刻准备着暑假作业原子能出版社系列答案 暑假衔接教材期末暑假预习武汉出版社系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案 假期作业暑假成长乐园新疆青少年出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案
相关题目
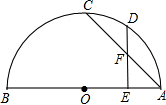 已知:如图,AB为⊙O的直径,C、D是半圆弧上的两点,E是AB上除O外的一点,AC与DE相交于F.①
已知:如图,AB为⊙O的直径,C、D是半圆弧上的两点,E是AB上除O外的一点,AC与DE相交于F.①
 =-
=- ,②DE⊥AB,③AF=DF.
,②DE⊥AB,③AF=DF.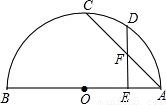
 ,②DE⊥AB,③AF=DF.
,②DE⊥AB,③AF=DF.
 ,②DE⊥AB,③AF=DF.
,②DE⊥AB,③AF=DF.