题目内容
如图，等腰△ABC中，AB=AC，∠B=40°，AC边的垂直平分线交BC于点E，连接AE，则∠BAE的度数是
- A.45°
- B.50°
- C.55°
- D.60°
D
分析：由于AB=AC，∠B=40°，根据等边对等角可以得到∠C=40°，又AC边的垂直平分线交BC于点E，根据线段的垂直平分线的性质得到AE=CE，再根据等边对等角得到∠C=40°=∠CAE，再根据三角形的内角和求出∠BAC即可求出∠BAE的度数．
解答：∵AB=AC，∠B=40°，
∴∠B=∠C=40°，
∴∠BAE=180°-∠B-∠C=100°，
又∵AC边的垂直平分线交BC于点E，
∴AE=CE，
∴∠CAE=∠C=40°，
∴∠BAE=∠BAE-∠CAE=60°．
故选D．
点评：此题考查了线段的垂直平分线的性质和等腰三角形的性质；利用角的等量代换是正确解答本题的关键．
分析：由于AB=AC，∠B=40°，根据等边对等角可以得到∠C=40°，又AC边的垂直平分线交BC于点E，根据线段的垂直平分线的性质得到AE=CE，再根据等边对等角得到∠C=40°=∠CAE，再根据三角形的内角和求出∠BAC即可求出∠BAE的度数．
解答：∵AB=AC，∠B=40°，
∴∠B=∠C=40°，
∴∠BAE=180°-∠B-∠C=100°，
又∵AC边的垂直平分线交BC于点E，
∴AE=CE，
∴∠CAE=∠C=40°，
∴∠BAE=∠BAE-∠CAE=60°．
故选D．
点评：此题考查了线段的垂直平分线的性质和等腰三角形的性质；利用角的等量代换是正确解答本题的关键．
练习册系列答案
相关题目
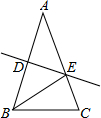如图，等腰△ABC中，AB=AC，∠A=20°．线段AB的垂直平分线交AB于D，交AC于E，连接BE，则∠CBE等于（ ）| A、80° | B、70° | C、60° | D、50° |
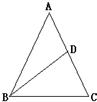13、如图，等腰△ABC中，AB=AC，BD为腰AC的中线，将△ABC分成长12cm和9cm的两段，则等腰△ABC的腰长为
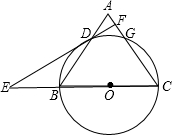如图，等腰△ABC中，AC=BC=10，AB=12，以BC为直径作⊙0交AB于D，交AC于G，DF⊥AC，垂足为F，交CB的延长线于点E，则sinE=
如图，等腰△ABC中，AB=AC，D为BC中点，E为射线AD上一点．
如图，等腰△ABC中，AB=AC，D、E分别为AC、AB的中点．