题目内容
【题目】如图,在△ABC中,AB=AC,以AC为直径的半圆O交BC于点E,DE⊥AB,垂足为D.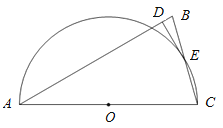
(1)求证:点E是BC的中点;
(2)判断DE与⊙O的位置关系,并证明你的结论;
(3)如果⊙O的直径为9,cosB=![]() , 求DE的长.
, 求DE的长.
【答案】
【解析】
(1)连接AE,根据等腰三角形的性质易证.
(2)相切,连接OE,证明OE⊥DE即可,根据三角形中位线定理证明.
(3)在Rt△ABE中,可由锐角三角函数定义可求BE的长;在Rt△BDE中,可由锐角三角函数定义和勾股定理可求DE的长.
【考点精析】关于本题考查的圆周角定理和直线与圆的三种位置关系,需要了解顶点在圆心上的角叫做圆心角;顶点在圆周上,且它的两边分别与圆有另一个交点的角叫做圆周角;一条弧所对的圆周角等于它所对的圆心角的一半;直线与圆有三种位置关系:无公共点为相离;有两个公共点为相交,这条直线叫做圆的割线;圆与直线有唯一公共点为相切,这条直线叫做圆的切线,这个唯一的公共点叫做切点才能得出正确答案.

练习册系列答案
相关题目