题目内容
 如图,平行于x轴的直线l与双曲线
如图,平行于x轴的直线l与双曲线 、
、 分别交于A、B两点,过A、B作x轴的垂线,垂足分别为C、D.若四边形ACDB的周长为8,且AB<AC,则点A的坐标是________.
分别交于A、B两点,过A、B作x轴的垂线,垂足分别为C、D.若四边形ACDB的周长为8,且AB<AC,则点A的坐标是________.
( ,3)
,3)
分析:设A点坐标为(a, ),利用AB平行于x轴,点B的纵坐标为
),利用AB平行于x轴,点B的纵坐标为 ,而点B在反比例函数y=-
,而点B在反比例函数y=- ,图象上,易得B点坐标为(-2a,
,图象上,易得B点坐标为(-2a, ),则AB=a-(-2a)=3a,AC=
),则AB=a-(-2a)=3a,AC= ,然后根据矩形的性质得到AB+AC=4,即3a+
,然后根据矩形的性质得到AB+AC=4,即3a+ =4,则3a2-4a+1=0,用因式分解法解得a1=
=4,则3a2-4a+1=0,用因式分解法解得a1= ,a2=1,而AB<AC,则a=
,a2=1,而AB<AC,则a= ,即可写出A点坐标.
,即可写出A点坐标.
解答:点A在反比例函数y= 图象上,设A点坐标为(a,
图象上,设A点坐标为(a, ),
),
∵AB平行于x轴,
∴点B的纵坐标为 ,
,
而点B在反比例函数y=- ,图象上,
,图象上,
∴B点的横坐标=-2×a=-2a,即B点坐标为(-2a, ),
),
∴AB=a-(-2a)=3a,AC= ,
,
∵四边形ABCD的周长为8,而四边形ABCD为矩形,
∴AB+AC=4,即3a+ =4,
=4,
整理得,3a2-4a+1=0,(3a-1)(a-1)=0,
∴a1= ,a2=1,
,a2=1,
而AB<AC,
∴a= ,
,
∴A点坐标为( ,3),
,3),
故答案为:( ,3).
,3).
点评:本题考查了反比例函数综合题,要求同学们掌握点在反比例函数图象上,点的横纵坐标满足其解析式,解答本题的关键是利用矩形对边相等的性质建立方程以及用因式分解法解一元二次方程.
 ,3)
,3)分析:设A点坐标为(a,
 ),利用AB平行于x轴,点B的纵坐标为
),利用AB平行于x轴,点B的纵坐标为 ,而点B在反比例函数y=-
,而点B在反比例函数y=- ,图象上,易得B点坐标为(-2a,
,图象上,易得B点坐标为(-2a, ),则AB=a-(-2a)=3a,AC=
),则AB=a-(-2a)=3a,AC= ,然后根据矩形的性质得到AB+AC=4,即3a+
,然后根据矩形的性质得到AB+AC=4,即3a+ =4,则3a2-4a+1=0,用因式分解法解得a1=
=4,则3a2-4a+1=0,用因式分解法解得a1= ,a2=1,而AB<AC,则a=
,a2=1,而AB<AC,则a= ,即可写出A点坐标.
,即可写出A点坐标.解答:点A在反比例函数y=
 图象上,设A点坐标为(a,
图象上,设A点坐标为(a, ),
),∵AB平行于x轴,
∴点B的纵坐标为
 ,
,而点B在反比例函数y=-
 ,图象上,
,图象上,∴B点的横坐标=-2×a=-2a,即B点坐标为(-2a,
 ),
),∴AB=a-(-2a)=3a,AC=
 ,
,∵四边形ABCD的周长为8,而四边形ABCD为矩形,
∴AB+AC=4,即3a+
 =4,
=4,整理得,3a2-4a+1=0,(3a-1)(a-1)=0,
∴a1=
 ,a2=1,
,a2=1,而AB<AC,
∴a=
 ,
,∴A点坐标为(
 ,3),
,3),故答案为:(
 ,3).
,3).点评:本题考查了反比例函数综合题,要求同学们掌握点在反比例函数图象上,点的横纵坐标满足其解析式,解答本题的关键是利用矩形对边相等的性质建立方程以及用因式分解法解一元二次方程.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目

 相交于点C.
相交于点C.

 与x轴交于点A(—2,0),交y轴于点B(0,
与x轴交于点A(—2,0),交y轴于点B(0, ).直
).直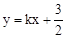 过点A与y轴交于点C,与抛物线的另一个交点是D.
过点A与y轴交于点C,与抛物线的另一个交点是D.
