Question

【题目】如图，中，∠，，的面积为，为边上一动点（不与，重合），将和分别沿直线，翻折得到和，那么△的面积的最小值为____．

Answer 1

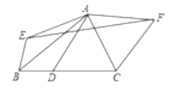
【答案】4.

【解析】

过E作EG⊥AF，交FA的延长线于G，由折叠可得∠EAG＝30°，而当AD⊥BC时，AD最短，依据BC＝7，△ABC的面积为14，即可得到当AD⊥BC时，AD＝4＝AE＝AF，进而得到△AEF的面积最小值为：AF×EG＝×4×2＝4.

解：如图，过E作EG⊥AF，交FA的延长线于G，

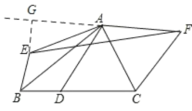
由折叠可得，AF＝AE＝AD，∠BAE＝∠BAD，∠DAC＝∠FAC，
∵∠BAC＝75°，
∴∠EAF＝150°，
∴∠EAG＝30°，
∴EG＝AE＝AD，
当AD⊥BC时，AD最短，
∵BC＝7，△ABC的面积为14，
∴当AD⊥BC时，

，

即：，

∴.
∴△AEF的面积最小值为：
AF×EG＝×4×2＝4，

故答案为：4.