题目内容
已知任意三角形ABC，其面积为S．作BC的平行线与AB、AC分别交于D、E．设三角形BDE的面积为M，求证：M≤| 1 | 4 |
分析：由于△ADE与△BDE是等高的三角形，可得
=
，同理亦可得
=
，
=
再由平行线分线段成比例的性质可得M与S的关系，进而即可求解．
| M |
| S△ADE |
| BD |
| AD |
| S△ADE |
| S△ABE |
| AD |
| AB |
| S△ABE |
| S |
| AE |
| AC |
解答：证明：由于△ADE与△BDE是等高的三角形，
故
=
=
=
-1(1)
又△ADE与△ABE也是等高三角形，
故
=
（2）
同理，
=
（3）
又DE∥BC，故
=
，设此比值为x
将（1），（2），（3）式相乘，
得
=(
-1)•
•
=(1-
)
即
=(1-x)x
法一：展开得Sx2-Sx+M=0有实根，
故△=S2-4SM≥0
解之得M≤
S
法二：由
=(1-x)x=
-(x-
)2 ≤
?M≤
S．
故
| M |
| S△ADE |
| BD |
| AD |
| AB-AD |
| AD |
| AB |
| AD |
又△ADE与△ABE也是等高三角形，
故
| S△ADE |
| S△ABE |
| AD |
| AB |
同理，
| S△ABE |
| S |
| AE |
| AC |
又DE∥BC，故
| AD |
| AB |
| AE |
| AC |
将（1），（2），（3）式相乘，
得
| M |
| S |
| AB |
| AD |
| AD |
| AB |
| AE |
| AC |
| AD |
| AB |
| AD |
| AB |
即
| M |
| S |
法一：展开得Sx2-Sx+M=0有实根，
故△=S2-4SM≥0
解之得M≤
| 1 |
| 4 |
法二：由
| M |
| S |
| 1 |
| 4 |
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 4 |
点评：本题主要考查了平行线分线段成比例的性质以及三角形的面积问题，能够熟练求解．
练习册系列答案
相关题目
25、已知任意三角形△ABC，顺次连接△ABC各边中点得到△A1B1C1再顺次连接△A1B1C1各边中点得△A2B2C2，若△ABC周长为4cm，则△ABC、△A1B1C1、△A2B2C2周长之和为
已知任意三角形ABC，其面积为S．作BC的平行线与AB、AC分别交于D、E．设三角形BDE的面积为M，求证：M≤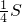
．
