题目内容
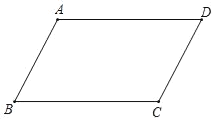
【题目】如图，矩形ABCD中，AB＝2，BC＝4，对角线AC的垂直平分线分别交AD、BC于点E、F，连接CE，则△DCE的面积为（ ）
A. 
B. 
C. 2D. 1
【答案】B
【解析】
由EF垂直平分AC可得AE=CE，设CE＝x，则ED＝AD﹣AE＝4﹣x，在Rt△CDE中，利用勾股定理求出x的长，继而根据三角形的面积公式进行求解即可.
∵四边形ABCD是矩形，
∴CD＝AB＝2，AD＝BC＝4，∠D=90°，
∵EO是AC的垂直平分线，
∴AE＝CE，
设CE＝x，则ED＝AD﹣AE＝4﹣x，
在Rt△CDE中，CE2＝CD2+ED2，
即x2＝22+(4﹣x)2，
解得：x＝
，
即CE的长为，
DE＝4﹣＝
，
所以△DCE的面积＝
××2＝，
故选B．
练习册系列答案
相关题目
【题目】某商场经营一批进价2元的小商品，在经营中发现此商品的日销售单价与日销量之间的关系如表：
日销售单价（元） | 3 | 5 | 7 | 9 | 11 |
日销量（件） | 18 | 14 | 10 | 6 | 2 |
（1）上表反映了日销售单价与日销量之间的关系，其中 是自变量， 是因变量．
（2）如果用x表示日销售单价，y表示日销量，那么y与x之间的关系式是 ；
（3）日销售单价为 元时，商场日销售盈利最高？（盈利
日销售总额-日销售商品的总进价）
