题目内容
已知△ABC为等边三角形,BD为中线,延长BC至E,使CE=CD=1,连接DE,则DE= ![]() .
.

考点:
等边三角形的性质;等腰三角形的判定与性质.
分析:
根据等腰三角形和三角形外角性质求出BD=DE,求出BC,在Rt△△BDC中,由勾股定理求出BD即可.
解答:
解:∵△ABC为等边三角形,
∴∠ABC=∠ACB=60°,AB=BC,
∵BD为中线,
∴∠DBC=∠ABC=30°,
∵CD=CE,
∴∠E=∠CDE,
∵∠E+∠CDE=∠ACB,
∴∠E=30°=∠DBC,
∴BD=DE,
∵BD是AC中线,CD=1,
∴AD=DC=1,
∵△ABC是等边三角形,
∴BC=AC=1+1=2,BD⊥AC,
在Rt△△BDC中,由勾股定理得:BD=![]() =
=![]() ,
,
即DE=BD=![]() ,
,
故答案为:![]() .
.
点评:
本题考查了等边三角形性质,勾股定理,等腰三角形性质,三角形的外角性质等知识点的应用,关键是求出DE=BD和求出BD的长.

练习册系列答案
相关题目
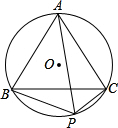 已知△ABC是等边三角形,⊙O为它的外接圆,点P是
已知△ABC是等边三角形,⊙O为它的外接圆,点P是

 已知D是等边△ABC外一点,∠BDC=120°,则AD、BD、DC三条线段的数量关系为
已知D是等边△ABC外一点,∠BDC=120°,则AD、BD、DC三条线段的数量关系为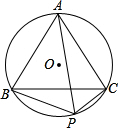 已知△ABC是等边三角形,⊙O为它的外接圆,点P是
已知△ABC是等边三角形,⊙O为它的外接圆,点P是 上任一点.
上任一点. 上任一点.
上任一点.