题目内容
(10分) 如图8, △ABC是等边三角形,D是BC延长线上任意一点,以AD为一边向右侧作等边△ADE,连接CE.
(1)求证:△CAE≌△BAD;
(2)判断直线AB与EC的位置关系,并说明理由.
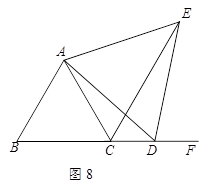
(1)∵△ADE与△ABC都是等边三角形,
∴ AC = AB,AE = AD,∠DAE =∠BAC =60°.
∴ ∠DAE+∠CAD=∠BAC+∠CAD. 即 ∠CAE =∠BAD.
∴ △CAE≌△BAD.
(2)EC∥AB.
由△CAE≌△BAD, ∴ ∠ACE=∠B=60°, ∴ ∠ACE=∠BAC=60°,
∴ EC∥AB.
解析:略

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 3、某校为了了解学生的身体素质情况,对初三(2)班的50名学生进行了立定跳远、铅球、100米三个项目的测试,每个项目满分为10分.如图,是将该学生所得的三项成绩(成绩均为整数)之和进行整理后,分成5组画出的频率分布直方图,已知从左至右前4个小组的频率分别为0.02,0.1,0.12,0.46.
3、某校为了了解学生的身体素质情况,对初三(2)班的50名学生进行了立定跳远、铅球、100米三个项目的测试,每个项目满分为10分.如图,是将该学生所得的三项成绩(成绩均为整数)之和进行整理后,分成5组画出的频率分布直方图,已知从左至右前4个小组的频率分别为0.02,0.1,0.12,0.46.

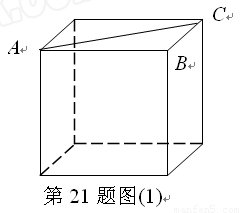

 与平面展开图中
与平面展开图中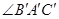 的大小关系?
的大小关系?