题目内容
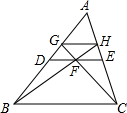如图，已知DE是△ABC的中位线，F是DE的中点，连接BF并延长交AC于H，连结CF并延长交AD于G，则GH：DE=________．
2：3
分析：根据三角形中位线得出ED∥BC，
=
，①求出
=
=
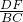，证△GFD∽△GCB，△HFE∽△HBC，推出
==，
=
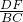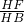=，求出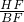
=
=
，证△GFH∽△CFB，得出
=，②，②÷①即可得出答案．
解答：∵DE是△ABC的中位线，
∴ED∥BC，=，①
∵F为DE中点，
∴==，
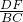∵DE∥BC，
∴△GFD∽△GCB，△HFE∽△HBC，
∴==，==，
∴
=
=，
∴==，
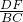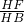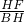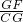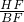∵∠GFH=∠BFC，
∴△GFH∽△CFB，
∴=，②，
②÷①得：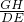
=
，
故答案为：2：3．
点评：本题考查了相似三角形的性质和判定，三角形的中位线的应用，关键是能求出DE：BC=1：2，GH：BC=1：3．
分析：根据三角形中位线得出ED∥BC，
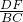=，①求出==，证△GFD∽△GCB，△HFE∽△HBC，推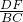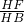出==，==，求出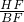==，证△GFH∽△CFB，得出=，②，②÷①即可得出答案．解答：∵DE是△ABC的中位线，
∴ED∥BC，
=，①∵F为DE中点，
∴
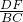==，∵DE∥BC，
∴△GFD∽△GCB，△HFE∽△HBC，
∴
==，==，∴
==，∴
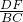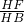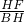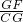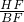==，∵∠GFH=∠BFC，
∴△GFH∽△CFB，
∴
=，②，②÷①得：
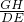=，故答案为：2：3．
点评：本题考查了相似三角形的性质和判定，三角形的中位线的应用，关键是能求出DE：BC=1：2，GH：BC=1：3．
练习册系列答案
出彩同步大试卷系列答案
相关题目
17、如图，已知DE是AC的垂直平分线，AB=10cm，BC=11cm，则△ABD的周长为
如图，已知DE是△ABC的一条中位线，F、G分别是线段BD、CE的中点，若FG=6，则BC=
如图，已知DE是直角梯形ABCD的高，将△ADE沿DE翻折，腰AD恰好经过腰BC的中点，则AE：BE等于（ ）
30°．