题目内容
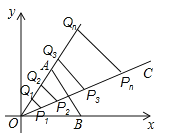
【题目】如图，在直角坐标系xOy中，点A在第一象限，点B在x轴的正半轴上，△AOB为正三角形，射线OC⊥AB，在OC上依次截取点P1，P2，P3，…，Pn，使OP1=1，P1P2=3，P2P3=5，…，Pn﹣1Pn=2n﹣1（n为正整数），分别过点P1，P2，P3，…，Pn向射线OA作垂线段，垂足分别为点Q1，Q2，Q3，…，Qn，则点Qn的坐标为 ．
【答案】（
，
）．
【解析】
试题分析：∵△AOB为正三角形，射线OC⊥AB，∴∠AOC=30°，又∵Pn﹣1Pn=2n﹣1，PnQn⊥OA，∴OQn=
（OP1+P1P2+P2P3+…+Pn﹣1Pn）=（1+3+5+…+2n﹣1）=
，∴Qn的坐标为（cos60°，sin60°），∴Qn的坐标为（，）．故答案为：（，）．
练习册系列答案
名师金手指领衔课时系列答案
相关题目
