题目内容
如图9-1,已知ABCD是边长为4的正方形,E是CD边上的一个动点,连接AE,AE的延长线交BC的延长线于点P,连接PD.作△ADE的外接圆⊙O.设DE = x,PC = y.
(1)求y与x之间的函数关系式;(2分)
(2)若PD是⊙O的切线,求x的值.(4分)
(3)过点D作DF⊥AE,垂足为H,交⊙O于点F,直线AF交BC于点G(如图9-2).若x=2,则sin∠BAG的值是_________.(2分)


(1)解:∵四边形ABCD是正方形
∴AD//BC
∴∠ADE =∠PCE,∠DAE=∠CPE
∴△ADE∽△PCE………………1分
∴![]()
∴![]()
∴![]() ……………………2分
……………………2分
(2)解:连接OD

∵∠ADE=90º,AE是⊙O的直径
∵PD是⊙O的切线,∴PD⊥OD
∴∠PDO+∠ODE=90º……………… 3分
∵∠PEC+∠CPE=90º,∠PEC=∠OED
∴∠OED+∠CPE=90º
∵OD=OE,∴∠OED=∠ODE
∴∠CPE=∠PDC…………………………………………………………4分
∵∠PCE=∠PCD
∴△PCE∽△DCP,∴![]() …………………………………………5分
…………………………………………5分
∴![]() ,即
,即![]()
由(1)知![]() ,∴
,∴![]()
解得![]() 或
或![]() (不合题意,舍去)
(不合题意,舍去)
∴x= ………………………………………………………………6分
………………………………………………………………6分
(3)解:sin∠BAG=![]() .…………………………………………………………8分
.…………………………………………………………8分
解析:略

练习册系列答案
 心算口算巧算一课一练系列答案
心算口算巧算一课一练系列答案 应用题作业本系列答案
应用题作业本系列答案
相关题目
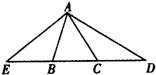
 20、如图所示,已知AB=AC,PB=PC,下面结论:(1)EB=EC;(2)AD⊥BC;(3)AE平分∠BEC;(4)∠PBC=∠PCB,其中正确的是( )
20、如图所示,已知AB=AC,PB=PC,下面结论:(1)EB=EC;(2)AD⊥BC;(3)AE平分∠BEC;(4)∠PBC=∠PCB,其中正确的是( )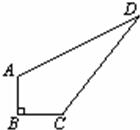 20、某住宅小区有一块草坪如图所示.已知AB=3米,BC=4米,CD=12米,DA=13米,且AB⊥BC,求这块草坪的面积.
20、某住宅小区有一块草坪如图所示.已知AB=3米,BC=4米,CD=12米,DA=13米,且AB⊥BC,求这块草坪的面积.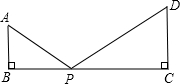 如图所示,已知AB⊥BC于B,CD⊥BC于C,AB=4,CD=6,BC=14,P为BC上一点,试问BP为何值时,△ABP与△PCD相似?
如图所示,已知AB⊥BC于B,CD⊥BC于C,AB=4,CD=6,BC=14,P为BC上一点,试问BP为何值时,△ABP与△PCD相似? 如图所示,已知AB为⊙O的直径,CD是弦,且AB⊥CD,垂足为E.连接AC,OC,BC,若EB=8cm,CD=24cm,则⊙O的直径为
如图所示,已知AB为⊙O的直径,CD是弦,且AB⊥CD,垂足为E.连接AC,OC,BC,若EB=8cm,CD=24cm,则⊙O的直径为