题目内容
 如图,在等腰△ABC中,AB=AC,一腰上中线BD将这个三角形的周长分为16和8的两部分,求这个等腰三角形的腰长与底边长.(用方程思想解决)
如图,在等腰△ABC中,AB=AC,一腰上中线BD将这个三角形的周长分为16和8的两部分,求这个等腰三角形的腰长与底边长.(用方程思想解决)分析:设等腰三角形的腰长为x,底边为y,然后分两种情况列出方程组,求解即可.
解答:解:设等腰三角形的腰长为x,底边为y,
根据题意得,
或
,
解得
或
,
为腰长,
为底边时,
+
=
<
,
不能组成三角形,
所以,这个等腰三角形的腰长是
,底边长是
.
根据题意得,
|
|
解得
|
|
| 16 |
| 3 |
| 40 |
| 3 |
| 16 |
| 3 |
| 16 |
| 3 |
| 32 |
| 3 |
| 40 |
| 3 |
不能组成三角形,
所以,这个等腰三角形的腰长是
| 32 |
| 3 |
| 8 |
| 3 |
点评:本题考查了等腰三角形的性质,三角形的三边关系,根据等腰三角形的两腰相等列出方程组是解题的关键,难点在于要分情况讨论并利用三角形的三边关系判断是否能组成三角形.

练习册系列答案
相关题目
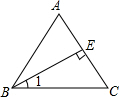 如图,在等腰△ABC中,AB=AC,BE⊥AC,垂足为E,则∠1与∠A的关系式为( )
如图,在等腰△ABC中,AB=AC,BE⊥AC,垂足为E,则∠1与∠A的关系式为( )| A、∠1=∠A | ||
B、∠1=
| ||
| C、∠1=2∠A | ||
| D、无法确定 |
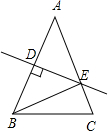 如图,在等腰△ABC中,AB=AC,AB的垂直平分线DE交AB于点D,交另一腰AC于点E,若∠EBC=15°,则∠A=
如图,在等腰△ABC中,AB=AC,AB的垂直平分线DE交AB于点D,交另一腰AC于点E,若∠EBC=15°,则∠A=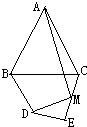 24、如图,在等腰△ABC中,AB=AC,∠ABC=α,在四边形BDEC中,DB=DE,∠BDE=2α,M为CE的中点,连接AM,DM.
24、如图,在等腰△ABC中,AB=AC,∠ABC=α,在四边形BDEC中,DB=DE,∠BDE=2α,M为CE的中点,连接AM,DM.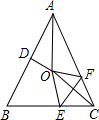 (2012•丽水)如图,在等腰△ABC中,AB=AC,∠BAC=50°.∠BAC的平分线与AB的中垂线交于点O,点C沿EF折叠后与点O重合,则∠CEF的度数是
(2012•丽水)如图,在等腰△ABC中,AB=AC,∠BAC=50°.∠BAC的平分线与AB的中垂线交于点O,点C沿EF折叠后与点O重合,则∠CEF的度数是 如图,在等腰△ABC中,AB=AC=10cm,直线DE垂直平分AB,分别交AB、AC于D、E两点.若BC=8cm,则△BCE的周长是
如图,在等腰△ABC中,AB=AC=10cm,直线DE垂直平分AB,分别交AB、AC于D、E两点.若BC=8cm,则△BCE的周长是