题目内容
若方程x2+x-1=0的两实根为α、β,那么下列说法不正确的是( )
| A、α+β=-1 | ||||
| B、αβ=-1 | ||||
| C、α2+β2=3 | ||||
D、
|
考点:根与系数的关系
专题:计算题
分析:先根据根与系数的关系得到α+β=-1,αβ=-1,再利用完全平方公式变形α2+β2得到(α+β)2-2αβ,利用通分变形
+
得到
,然后利用整体代入的方法分别计算两个代数式的值,这样可对各选项进行判断.
| 1 |
| α |
| 1 |
| β |
| α+β |
| αβ |
解答:解:根据题意得α+β=-1,αβ=-1.
所以α2+β2=(α+β)2-2αβ=(-1)2-2×(-1)=3;
+
=
=
=1.
故选:D.
所以α2+β2=(α+β)2-2αβ=(-1)2-2×(-1)=3;
| 1 |
| α |
| 1 |
| β |
| α+β |
| αβ |
| -1 |
| -1 |
故选:D.
点评:本题考查了一元二次方程ax2+bx+c=0(a≠0)的根与系数的关系:若方程两个为x1,x2,则x1+x2=-
,x1•x2=
.
| b |
| a |
| c |
| a |

练习册系列答案
 中考利剑中考试卷汇编系列答案
中考利剑中考试卷汇编系列答案 教育世家状元卷系列答案
教育世家状元卷系列答案 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案 单元加期末复习先锋大考卷系列答案
单元加期末复习先锋大考卷系列答案
相关题目
 如图,一次函数y=(m-1)x-m的图象分别与x轴、y轴的负半轴相交于A、B,则m的取值范围是( )
如图,一次函数y=(m-1)x-m的图象分别与x轴、y轴的负半轴相交于A、B,则m的取值范围是( )| A、m>1或m<0 | B、0<m<1 |
| C、m<0 | D、m>1 |
 已知的图象如图所示,当y<0时,x的取值范围是( )
已知的图象如图所示,当y<0时,x的取值范围是( )| A、x>-3 | B、x<-3 |
| C、x>1 | D、x<1 |
某商品原价5元,如果跌价x%后,仍不低于4元,那么( )
| A、x≤20 | B、x<20 |
| C、x≥20 | D、x>20 |
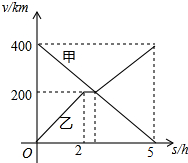 甲,乙两辆汽车分别从A,B两地同时出发,沿同一条公路相向而行,乙车出发2h后休息,与甲车相遇后,继续行驶.设甲、乙两车与B地的路程分别为y甲(km),y乙(km),甲车行驶的时间为x(h),y甲,y乙与x之间的函数图象如图所示,结合图象解答下列问题:
甲,乙两辆汽车分别从A,B两地同时出发,沿同一条公路相向而行,乙车出发2h后休息,与甲车相遇后,继续行驶.设甲、乙两车与B地的路程分别为y甲(km),y乙(km),甲车行驶的时间为x(h),y甲,y乙与x之间的函数图象如图所示,结合图象解答下列问题: