题目内容
【题目】人们在长期的数学实践中总结了许多解决数学问题的方法,形成了许多光辉的数学想法,其中转化思想是中学教学中最活跃,最实用,也是最重要的数学思想,例如将不规则图形转化为规则图形就是研究图形问题比较常用的一种方法。
问题提出:求边长分别为![]() 的三角形面积。
的三角形面积。
问题解决:在解答这个问题时,先建立一个正方形网格(每个小正方形的边长为1),再在网格中画出边长分别为![]() 的格点三角形△ABC(如图①),AB=
的格点三角形△ABC(如图①),AB=![]() 是直角边为1和2的直角三角形斜边,BC=
是直角边为1和2的直角三角形斜边,BC=![]() 是直角边分别为1和3的直角三角形的斜边,AC=
是直角边分别为1和3的直角三角形的斜边,AC=![]() 是直角边分别为2和3 的直角三角形斜边,用一个大长方形的面积减去三个直角三角形的面积,这样不需求△ABC的高,而借用网格就能计算出它的面积。
是直角边分别为2和3 的直角三角形斜边,用一个大长方形的面积减去三个直角三角形的面积,这样不需求△ABC的高,而借用网格就能计算出它的面积。
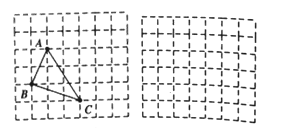
(1)请直接写出图①中△ABC的面积为_______________ 。
(2)类比迁移:求边长分别为![]() 的三角形面积(请利用图②的正方形网格画出相应的△ABC,并求出它的面积)。
的三角形面积(请利用图②的正方形网格画出相应的△ABC,并求出它的面积)。
【答案】(1)![]() ;(2)3
;(2)3
【解析】(1)利用割补法即可求出面积;
(2)先利用勾股定理画出以这三条线段为边的三角形,再利用割补法即可求出面积.
解:(1)S△ABC=3×3-![]() ×1×2-
×1×2-![]() ×1×3-
×1×3-![]() ×2×3=
×2×3=![]() ;
;
故答案为:![]()
(2)在网格中画出边长分别为![]() 格点三角形△ABC.AB=
格点三角形△ABC.AB=![]() 是直角边为1和2的直角三角形斜边,AC=
是直角边为1和2的直角三角形斜边,AC=![]() 是直角边分别为2和2的直角三角形的斜边,BC=
是直角边分别为2和2的直角三角形的斜边,BC=![]() 是直角边分别为1和4 的直角三角形斜边,则△ABC可看作一个边长分别为2和4的矩形减去三个直角三角形得到的:
是直角边分别为1和4 的直角三角形斜边,则△ABC可看作一个边长分别为2和4的矩形减去三个直角三角形得到的:
所以S△ABC=2×4-![]() ×1×2-
×1×2-![]() ×1×4-
×1×4-![]() ×2×2=3.
×2×2=3.


练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目