Question

【题目】如图，抛物线y=x2+bx+c经过A（-1，0），C（2，-3）两点，与y轴交于点D，与x轴交于另一点B．

（1）求此抛物线的解析式及顶点坐标；

（2）若将此抛物线平移，使其顶点为点D，需如何平移？写出平移后抛物线的解析式；

（3）过点P（m，0）作x轴的垂线（1≤m≤2），分别交平移前后的抛物线于点E，F，交直线OC于点G，求证：PF=EG．

Answer 1

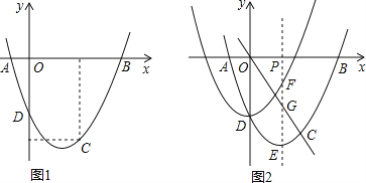
【答案】（1），（，）；（2）向左个单位长度，再向上平移个单位长度．平移后的抛物线解析式为：．（3）证明见解析.

【解析】

试题（1）把A（-1，0），C（2，-3）代入y=x2+bx+c，得到关于b、c的二元一次方程组，解方程组求出b、c的值，即可求出抛物线的解析式，再利用配方法将一般式化为顶点式，即可求出顶点坐标；

（2）先求出抛物线y=x2-x-2与y轴交点D的坐标为（0，-2），再根据平移规律可知将点（，-）向左平移个单位长度，再向上平移个单位长度，可得到点D，然后利用顶点式即可写出平移后的抛物线解析式为：y=x2-2；

（3）先用待定系数法求直线OC的解析式为y=-x，再将x=m代入，求出yG=-m，yF=m2-2，yE=m2-m-2，再分别计算得出PF=-（m2-2）=2-m2，EG=yG-yE=2-m2，由此证明PF=EG．

试题解析：（1）解：把A（-1，0），C（2，-3）代入y=x2+bx+c，

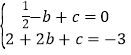得：，解得：，

∴抛物线的解析式为：，

∵=，

∴其顶点坐标为：（，-）；

（2）解：∵

∴当x=0时，y=-2，

∴D点坐标为（0，-2）．

∵将点（，-）向左平移个单位长度，再向上平移个单位长度，可得到点D，

∴将向左平移个单位长度，再向上平移个单位长度，顶点为点D，

此时平移后的抛物线解析式为：；

（3）证明：设直线OC的解析式为y=kx，

∵C（2，-3），

∴2k=-3，解得k=-，

∴直线OC的解析式为y=-x．

当x=m时，yF=m2-2，则PF=-（m2-2）=2-m2，

当x=m时，yE=m2-m-2，yG=-m，

则EG=yG-yE=2-m2，

∴PF=EG．