题目内容
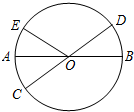 如图,已知AB、CD是⊙O的直径,
如图,已知AB、CD是⊙O的直径,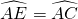 ,∠AOE=32°,那么∠COE的度数为________度.
,∠AOE=32°,那么∠COE的度数为________度.
64
分析:根据等弧所对的圆心角相等求得∠AOE=∠COA=32°,所以∠COE=∠AOE+∠COA=64°.
解答:∵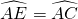 ,(已知)
,(已知)
∴∠AOE=∠COA(等弧所对的圆心角相等);
又∠AOE=32°,
∴∠COA=32°,
∴∠COE=∠AOE+∠COA=64°.
故答案是:64°.
点评:本题考查了圆心角、弧、弦的关系.在同圆或等圆中,两个圆心角、两条弧、两条弦三组量之间,如果有一组量相等,那么,它们所对应的其它量也相等.
分析:根据等弧所对的圆心角相等求得∠AOE=∠COA=32°,所以∠COE=∠AOE+∠COA=64°.
解答:∵
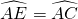 ,(已知)
,(已知)∴∠AOE=∠COA(等弧所对的圆心角相等);
又∠AOE=32°,
∴∠COA=32°,
∴∠COE=∠AOE+∠COA=64°.
故答案是:64°.
点评:本题考查了圆心角、弧、弦的关系.在同圆或等圆中,两个圆心角、两条弧、两条弦三组量之间,如果有一组量相等,那么,它们所对应的其它量也相等.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
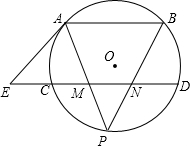 如图,已知AB、CD是⊙O的两条平行弦,过A点的⊙O的切线AE和DC的延长线交于E点,P为弧
如图,已知AB、CD是⊙O的两条平行弦,过A点的⊙O的切线AE和DC的延长线交于E点,P为弧

 11、如图,已知AB=BC=CD=AD,∠DAC=40°,那么∠B=
11、如图,已知AB=BC=CD=AD,∠DAC=40°,那么∠B= 如图,已知AB,CD相交于点0,△ACO≌△BD0,CE∥DF,求证:CE=DF.
如图,已知AB,CD相交于点0,△ACO≌△BD0,CE∥DF,求证:CE=DF. 如图,已知AB、CD相交于点O,OE⊥AB,∠EOC=28°,则∠AOD=
如图,已知AB、CD相交于点O,OE⊥AB,∠EOC=28°,则∠AOD=