题目内容
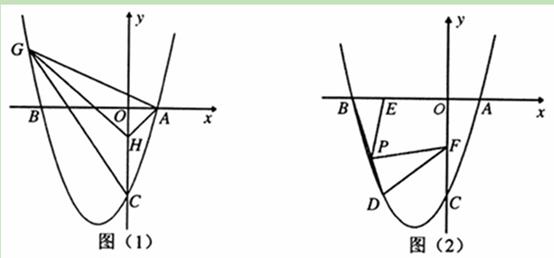
（11·十堰）12分）如图，已知抛物线y=x2+bx+c与x轴交于点A（1，0）和点B，与y轴交于点C（0，-3）。（1）求抛物线的解析式；
（2）如图（1），已知点H（0，-1）.问在抛物线上是否存在点G（点G在y轴的左侧），使得S△GHC=S△GHA？若存在，求出点G的坐标，若不存在，请说明理由；
（3）如图（2），抛物线上点D在x轴上的正投影为点E（-2，0），F是OC的中点，连接DF，P为线段BD上的一点，若∠EPF=∠BDF，求线段PE的长.
所以抛物线的解析式是y=x2+2x-3
(2)解法一：假设抛物线上存在点G，设G（m,n）,显然，当n=-3时，△AGH不存在。
S△AGH= S△GHC，∴m+n+1=0,
∵点G在y轴的左侧，∴G（-1，-4）.
解法二：①如图①，当GH//AC时，点A，点C到GH的距离相等，所以S△AGH= S△GHC，可得AC的解析式为y=3x-3,∵GH//AC,得GH的解析式为y=3x-1.
∴G(-1,-4)
②如图②，当GH与AC不平行时，因为点A，C到直线GH的距离相等，所以直线GH
(3) 如图③，E(-2,0), ∴D点的横坐标是-2，点D在抛物线上，∴D（-2，-3）
∠BPE+∠EPF+∠FPD=∠DFP+∠PDF+∠FPD=180°，
∠EPF=∠PDF，∴∠BPE=∠DFP,可证△PBE∽△FDP,
解析:略
练习册系列答案
相关题目
