Question

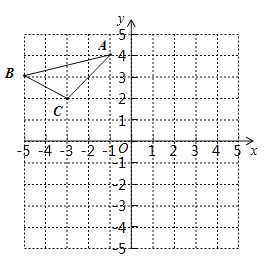
【题目】如图，点D是直角等腰△ABC斜边AB的中点，M为边AC上不和A、C重合的一动点，联结DM，过D作DNDM，交BC于N，联结MN．

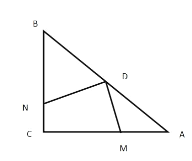
(1)求证：以AM、MN、BN为边的三角形是直角三角形

(2)如果AC2，AMx，试用x表示△DMN的面积，并求当ADM22．5时△DMN的面积．

Answer 1

【答案】（1）见解析；（2），

【解析】

（1）连接、MN，结合等腰直角三角形的性质利用ASA可证，由全等三角形的性质可得，，由是直角三角形可知以为边的三角形时直角三角形；

（2）易知，，由勾股定理可得MN长，由（1）中可知，结合勾股定理可知MD长，根据三角形面积公式可用x表示出△DMN的面积，当ADM22．5时，可得，在中，根据勾股定理可得CD长，求出x值代入△DMN的面积的表达式中即可求解.

（1） 如图，连接、MN，

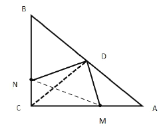
是等腰直角三角形

点D是AB的中点

在和中，

∴

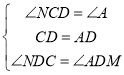
是直角三角形，即以为边的三角形时直角三角形

∴以为边的三角形时直角三角形

（2），由（1）知

在中，根据勾股定理得，

在中，根据勾股定理得

即 ，

所以

当时，，

，

在中，根据勾股定理得

由（1）知

，

，解得

将代入得.