题目内容
在同一直角坐标系中,由直线y=| 1 |
| 2 |
| 1 |
| 2 |
(1)求这个三角形的面积;
(2)过这个三角形的顶点能不能画出直线把这个三角形分成面积相等的两部分?若能,可以画出几条?写出这样的直线所对应的函数关系式.
分析:(1)分别求出两直线与x轴交点以及两直线之间的交点,然后根据三角形面积的求法算出这个三角形的面积;
(2)分别取三个顶点看是否存在符合题意的直线.
(2)分别取三个顶点看是否存在符合题意的直线.
解答: 解:(1)如图所示:
解:(1)如图所示:
直线y=
x+2、y=-
x+2和x轴以及两直线的交点坐标是:
A(-4,0),B(4,0),C(0,2),
所以AB=8,OC=2,
所以△ABC面积S=8;
(2)①以C为顶点,则该直线为:x=0;
②以A为顶点,则该直线过A和BC中点(2,2),
设该直线的解析式为:y=kx+b,代入两点坐标即可得到:y=
x+
;
③以B为顶点,同②解法相同,可得直线解析式为:y=-
x+
.
 解:(1)如图所示:
解:(1)如图所示:直线y=
| 1 |
| 2 |
| 1 |
| 2 |
A(-4,0),B(4,0),C(0,2),
所以AB=8,OC=2,
所以△ABC面积S=8;
(2)①以C为顶点,则该直线为:x=0;
②以A为顶点,则该直线过A和BC中点(2,2),
设该直线的解析式为:y=kx+b,代入两点坐标即可得到:y=
| 1 |
| 3 |
| 4 |
| 3 |
③以B为顶点,同②解法相同,可得直线解析式为:y=-
| 1 |
| 3 |
| 4 |
| 3 |
点评:本题主要考查对于一次函数图象的应用,要注意三角形面积的求法.

练习册系列答案
相关题目
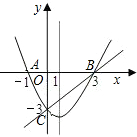 如图,在同一直角坐标系中,二次函数的图象与两坐标轴分别交于A(-1,0)、点B(3,0)和点C(0,-3),一次函数的图象与抛物线交于B、C两点.
如图,在同一直角坐标系中,二次函数的图象与两坐标轴分别交于A(-1,0)、点B(3,0)和点C(0,-3),一次函数的图象与抛物线交于B、C两点. 爱动脑筋的小明同学在买一双新的运动鞋时,发现了一些有趣现象,即鞋子的号码与鞋子的长(cm)之间存在着某种联系,经过收集数据,得到下表:
爱动脑筋的小明同学在买一双新的运动鞋时,发现了一些有趣现象,即鞋子的号码与鞋子的长(cm)之间存在着某种联系,经过收集数据,得到下表: