题目内容
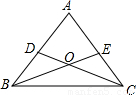
已知等腰△ABC的周长为36cm，底边BC上的高12cm，则cosB的值为
- A.
- B.
- C.
- D.
D
分析：设AB=xcm，则AC=AB=xcm，BC=（36-2x）cm，求出BD=DC=BC=（18-x）cm，在Rt△ADB中，由勾股定理得出方程x2=122+（18-x）2，求出x=13，求出AB=13cm，BD=5cm即可．
解答：
设AB=xcm，则AC=AB=xcm，BC=（36-2x）cm，
∵AB=AC，AD是高，
∴BD=DC=BC=（18-x）cm，
在Rt△ADB中，由勾股定理得：AB2=AD2+BD2，
x2=122+（18-x）2，
x=13，
即AB=13cm，BD=5cm，
∴cosB=
=，
故选D．
点评：本题考查了勾股定理，等腰三角形的性质，等腰直角三角形等知识点，关键是构造直角三角形和求出AB和BD的长，用了方程思想．
分析：设AB=xcm，则AC=AB=xcm，BC=（36-2x）cm，求出BD=DC=
BC=（18-x）cm，在Rt△ADB中，由勾股定理得出方程x2=122+（18-x）2，求出x=13，求出AB=13cm，BD=5cm即可．解答：
设AB=xcm，则AC=AB=xcm，BC=（36-2x）cm，
∵AB=AC，AD是高，
∴BD=DC=
BC=（18-x）cm，在Rt△ADB中，由勾股定理得：AB2=AD2+BD2，
x2=122+（18-x）2，
x=13，
即AB=13cm，BD=5cm，
∴cosB=
=，故选D．
点评：本题考查了勾股定理，等腰三角形的性质，等腰直角三角形等知识点，关键是构造直角三角形和求出AB和BD的长，用了方程思想．
练习册系列答案
相关题目
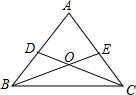在一次数学课上，周老师在屏幕上出示了一个例题：
在一次数学课上，周老师在屏幕上出示了一个例题：