题目内容
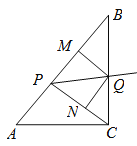
【题目】如图,已知,在Rt ![]() 中,斜边
中,斜边![]() ,
, ![]() ,点P为边AB上一动点(不与A,B重合),PQ平分
,点P为边AB上一动点(不与A,B重合),PQ平分![]() 交边BC于点Q,
交边BC于点Q, ![]() 于
于![]() 于N.
于N.
(1)当AP=CP时,求![]() ;
;
(2)若![]() ,求CQ;
,求CQ;
(3)探究:AP为何值时,四边形PMQN与![]() 的面积相等?
的面积相等?
【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]() 时,四边形PMQN与
时,四边形PMQN与![]() 的面积相等
的面积相等
【解析】分析:(1)由PQ为平分线,AP=CP,可得:PQ∥AC,再由AC⊥BC,PQ⊥BC,可得∠PCQ=∠PBQ即PC=PB,即可解出.(2)由△ABC的面积可得出PC的长,再由勾股定理列方程求出PB的长,MQ//PC推出 △BMQ∽△BPC,根据相似三角形性质解出结果;(3)(3)根据四边形PMQN和三角形△BPQ的面积相等得到QM是BP的垂直平分线,再由△CPQ∽△CBP即可作答.
本题解析:(1)在Rt ![]() 中,斜边
中,斜边![]() ,
, ![]() ,
,
![]() ,
, ![]() .
.
![]() ,
, ![]()
又∵PQ是∠BPC的平分线,
![]() ∴
∴![]()
又∵![]() ,
,![]()
![]() 为
为![]() 中点,
中点, ![]()
(2)![]() ,
,
![]()
![]() 得:
得: ![]() ,
,
设![]() 由勾股定理可列方程:
由勾股定理可列方程: ![]() ,
,
解得: ![]()
又![]()
![]() ,
,![]()
![]() ,
, ![]()
(3)由角平分线性质易得![]() ,
, ![]() ,
,
![]() 即
即![]() .∴QM是BP的垂直平分线,
.∴QM是BP的垂直平分线,
∴∠QPB=∠PBQ.∵∠QPB=∠CPQ∴∠PBQ=∠CPQ.
又∵∠PCQ=∠BCP,∴![]() .
.
![]() ,
,
![]() ,得
,得![]()
再由![]() 式得
式得![]() ,
,
![]() ,
,
![]()

练习册系列答案
相关题目
【题目】某天,一蔬菜经营户用120元钱按批发价从蔬菜批发市场买了西红柿和豆角共40kg,然后在市场上按零售价出售,西红柿和豆角当天的批发价和零售价如表所示:
品名 | 西红柿 | 豆角 |
批发价(单位:元/kg) | 2.4 | 3.2 |
零售价(单位:元/kg) | 3.8 | 5.2 |
如果西红柿和豆角全部以零售价售出,他当天卖这些西红柿和豆角赚了多少元钱?