题目内容
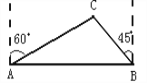
【题目】已知如图,在△ABC中,AB=AC,点D是线段BC上一个动点,以AD为腰在线段AD的右侧作△ADE,且AD=AE。
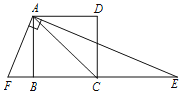
(1)如图①,当∠BAC=∠DAE=90°时,试判断线段BD和CE有什么关系,并给出证明:
(2)在(1)的条件下,若BC=4.试判断四边形ADCE的面积是否发生变化,若不变,求出四边形ADCE的面积;若变化,请说明理由;
(3)如图②,若∠BAC=∠DAE=120°,BC=4,试探索△DCE的面积是否存在最大值,若存在,求出此时∠DEC的度数,若不存在,请说明理由。
【答案】(1)BD=CE,证明见解析;(2)不变,4;(3)存在,60°.
【解析】
(1)根据同角的余角相等,可得∠BAD=∠CAE,运用“SAS”证明△ABD≌△ACE,根据全等三角形性质得出对应边相等,即可得到线段CE、BD之间的关系;
(2)由(1)得![]() ,所以
,所以 ![]() ,可得出四边形ADCE的面积不发生变化,根据等腰直角三角形的性质得出斜边BC上的高,即可求出面积;
,可得出四边形ADCE的面积不发生变化,根据等腰直角三角形的性质得出斜边BC上的高,即可求出面积;
(3)由![]()
![]() , 可得
, 可得![]() 的值最小时△DCE的面积存在最大值,由垂线段最短可得AD⊥BC时AD=AE的值最小,则
的值最小时△DCE的面积存在最大值,由垂线段最短可得AD⊥BC时AD=AE的值最小,则![]() 的值最小,根据全等三角形的性质和等腰三角形的性质即可求∠DEC的度数.
的值最小,根据全等三角形的性质和等腰三角形的性质即可求∠DEC的度数.
(1)BD=CE.
证明:∵∠BAC=∠DAE=90°,
∴∠BAD+∠DAC=∠CAE+∠DAC,
∴∠BAD=∠CAE,
在△DAB与△EAC中,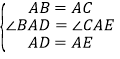
∴△DAB≌△EAC(SAS),
∴BD=CE;
(2)∵△DAB≌△EAC
∴![]()
∵![]()
∴![]() ,即四边形ADCE的面积不发生变化;
,即四边形ADCE的面积不发生变化;
∵∠BAC=90°,AB=AC,BC=4
∴Rt△ABC斜边上的高=2
∴![]()
![]()
(3)由(2)得![]()
![]()
∵![]()
![]()
∴![]() 的值最小时△DCE的面积存在最大值,
的值最小时△DCE的面积存在最大值,
由垂线段最短可得AD⊥BC时AD=AE的值最小,则![]() 的值最小,如下图,
的值最小,如下图,
∵∠BAC=∠DAE=120°,AB=AC,AD=AE
∴∠B=∠ACB=∠AED=30°, ∠BAD+∠DAC=∠CAE+∠DAC,
∴∠BAD=∠CAE,
在△DAB与△EAC中,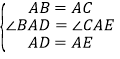
∴△DAB≌△EAC(SAS),
∵△DAB≌△EAC,AD⊥BC
∴∠AEC=∠ADB=90°
∴ ∠DEC=90°-30°=60°.
故答案为:(1)BD=CE,证明见解析;(2)不变,4;(3)存在,60°.

 阳光课堂课时优化作业系列答案
阳光课堂课时优化作业系列答案【题目】在学校组积的科学家素养竞赛中,每班参加比赛的人数相同,成绩分为A、B、C、D四个等级,其中相应等级的得分依次记为90分、80分、70 分、60 分,学校将八年级(1)班和(2) 班的成绩整理并绘制成如下的统计图:
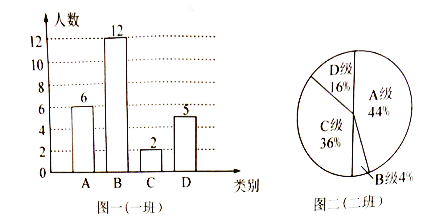
请你根据以上提供的信息解答下列问题:
(1) 此次竞赛中二 班成绩在70分以上(包括70分) 的人数有多少人?
(2) 补全下表中空缺的三个统计量:
平均数/ 分 | 中位数/ 分 | 众数/ 分 | |
一班 | 77.6 | 80 | _____________ |
二班 | _____________ | ______________ | 90 |
(3) 请根据上述图表对这次竞赛成绩进行分析,写出两个结论.