题目内容
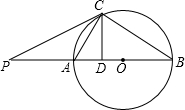 已知如图,点P是⊙O的直径BA延长线上一点,PC切⊙O于点C,连接CA,CB.
已知如图,点P是⊙O的直径BA延长线上一点,PC切⊙O于点C,连接CA,CB.
(1)求证:∠PCA=∠CBA;
(2)作CD⊥AB,垂足是D.求证:PA•PB=PD•PO.
 证明:(1)连接OC,∵PC切⊙O于点C,∠PCO=90°
证明:(1)连接OC,∵PC切⊙O于点C,∠PCO=90°∵BA是⊙O的直径,
∴∠ACB=90°,
∴∠PCA=∠OCB=∠CBA;
(2)∵∠PCA=∠CBA,且∠P是公共角,
∴△PBC∽△PCA,
∴
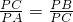
即PC2=PA•PB,
∵CD是直角△POC斜边上的高,
∴△PCD∽△POC;
∴
 ,
,即PC2=PD•PO,
∴PA•PB=PD•PO.
分析:(1)线连接OC,由已知PC切⊙O于点C可推出∠PCO=90°,再由AB是直径推出∠ACB=90°,所以∠PCA和∠CBA与∠AOC的和都是
90°通过等量代换得证;
(2)由已知通过证明△PBC∽△PCA和△PCD∽△POC得出结论;
点评:此题考查的知识点是切线的性质和相似三角形的判定、性质.关键是:
(1)由直径、切线得出两个直角通过等量代换得证,
(2)由已知通过证明△PBC∽△PCA和△PCD∽△POC得出结论;

练习册系列答案
相关题目
已知如图,点C是线段AB的黄金分割点(AC>BC),则下列结论中正确的是( )


| A、AB2=AC2+BC2 | ||||||
| B、BC2=AC•BA | ||||||
C、
| ||||||
D、
|
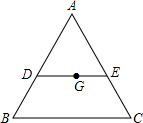 已知如图,点G是△ABC的重心,过点G作DE∥BC,分别交AB、AC于点D、E,那么S△ADE:S△ABC=
已知如图,点G是△ABC的重心,过点G作DE∥BC,分别交AB、AC于点D、E,那么S△ADE:S△ABC=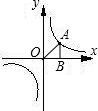 已知如图,点A是反比例函数y=
已知如图,点A是反比例函数y= 已知如图,点A是⊙O上一点.
已知如图,点A是⊙O上一点.
 B.
B.
 D.
D.