题目内容
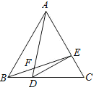
【题目】如图所示，点
是线段
的中点，
，
.
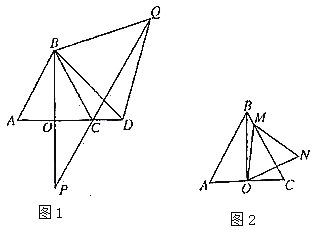
（1）如图1，若
，求证
是等边三角形；
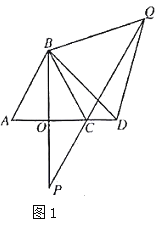
（2）如图1，在（1）的条件下，若点
在射线上，点在点
右侧，且
是等边三角形，
的延长线交直线
于点
，求
的长度；
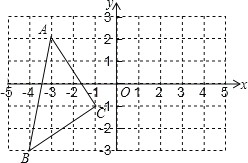
（3）如图2，在（1）的条件下，若点
在线段
上，
是等边三角形，且点沿着线段从点
运动到点，点
随之运动，求点的运动路径的长度.
【答案】（1）证明见解析；（2）18；（3）18.
【解析】
（1）利用垂直平分线的性质可得BA=BC，再得
，即可证明
是等边三角形；
（2）证明
，得出
，继而得到
，即可求得PC的长度；
（3）取BC的中点H，分两种情况证明
，得出
或
，可知点N的运动路径是一条线段，据此求解即可.
解：（1）∵
，
，
，
是线段
中点，，
，
是等边三角形；
（2）∵、
是等边三角形，
∴
，AB=BC，BD=BQ，
，
∴
，
∴，
，
，
，
，
，
；
（3）取BC的中点H，连接OH,连接CN，
分两种情况讨论：
当M在线段
上时，如图2，
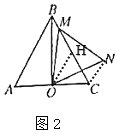
∵H是BC的中点，,
∴
,
∴
是等边三角形,
∵
是等边三角形,
∴
，OM=ON， 
，
∴
,
∴，
点
从起点到
作直线运动,
∵当点M在点B时，CN=BH=9,
∴点M从B运动到H时，点N运动路径的长度等于9；
当点M在线段
上时，如图3，
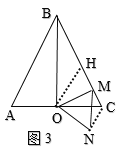
∵H是BC的中点，,
∴,
∴是等边三角形,
∵是等边三角形,
∴，OM=ON， ，
∴,
∴，
点从到终点作直线运动,
∵当点M在点C时，CN=CH=9,
∴点M从H运动到C时，点N运动路径的长度等于9；
综上所述，的路径长度为：
.
【题目】小迪同学在学勾股定理时发现一类特殊三角形：在一个三角形中，如果一个角是另一个角的2倍，那么称这个三角形为“倍角三角形”.
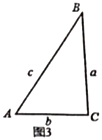
如图1，在倍角
中，
，
、
、
的对边分别记为
，
，
，三角形的三边，，有什么关系呢？让我们一起来探索……
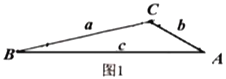
（1）已知“倍角三角形”的一个内角为
，则这个三角形的另两个角的度数分别为______
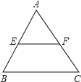
（2）小迪同学先从特殊的“倍角三角形”入手研究，请你结合图2和图3填写下表：
三角形 | 角的已知量 |
|
|
图2 |
| ______ | ______ |
图3 |
| ______ |
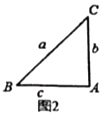
小迪同学根据上表，提出一般性猜想：在“倍角三角形”中，，那么，，三边满足：______；
（3）如图1：在倍角三角形中，
，、、的对边分别记为，，，求证：
.
