题目内容
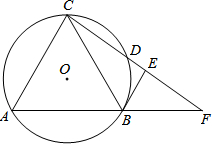 (2013•梧州一模)等边△ABC是⊙O的内接三角形,D是⊙O上一点,连接CD并延长交AB的延长线于点F,过点B作BE∥AC交CF于点E.
(2013•梧州一模)等边△ABC是⊙O的内接三角形,D是⊙O上一点,连接CD并延长交AB的延长线于点F,过点B作BE∥AC交CF于点E.(1)求证:BE是⊙O的切线;
(2)若AC=6,CD=4,求CF的值.
分析:(1)如图,连接BO并延长交⊙O于点G,连接CG.欲证明BE是⊙O的切线,只需证得GB⊥BE即可;
(2)如图,连接AD.构建相似三角形:△CFA∽△CAD.所以通过相似三角形的对应边成比例得到
=
,把相关线段的长度代入即可求得CF=
×6=9.
(2)如图,连接AD.构建相似三角形:△CFA∽△CAD.所以通过相似三角形的对应边成比例得到
| CF |
| CA |
| AC |
| DC |
| 6 |
| 4 |
解答: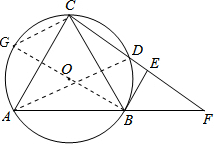 (1)证明:如图,连接BO并延长交⊙O于点G,连接CG.则∠BCG=90°,
(1)证明:如图,连接BO并延长交⊙O于点G,连接CG.则∠BCG=90°,
∵△ABC是等边三角形,
∴∠CAB=∠ACB=60°,
∴∠CGB=∠CAB=60°
∴∠CBG=30°.
∵AC∥BE
∴∠CBE=∠ACB=60°
∴∠CBE+∠CBG=∠GBE=90°,
∴BE是⊙O的切线;
(2)解:如图,连接AD.则∠ADC=∠ABC.
∵∠ABC=∠BAC=60°
∴∠BAC=∠ADC=60°,
∵∠ACD=∠FCA
∴△CFA∽△CAD
∴
=
.
∵AC=6,CD=4
∴CF=
×6=9.
 (1)证明:如图,连接BO并延长交⊙O于点G,连接CG.则∠BCG=90°,
(1)证明:如图,连接BO并延长交⊙O于点G,连接CG.则∠BCG=90°,∵△ABC是等边三角形,
∴∠CAB=∠ACB=60°,
∴∠CGB=∠CAB=60°
∴∠CBG=30°.
∵AC∥BE
∴∠CBE=∠ACB=60°
∴∠CBE+∠CBG=∠GBE=90°,
∴BE是⊙O的切线;
(2)解:如图,连接AD.则∠ADC=∠ABC.
∵∠ABC=∠BAC=60°
∴∠BAC=∠ADC=60°,
∵∠ACD=∠FCA
∴△CFA∽△CAD
∴
| CF |
| CA |
| AC |
| DC |
∵AC=6,CD=4
∴CF=
| 6 |
| 4 |
点评:本题考查了切线的判定,相似三角形的判定与性质.要证某线是圆的切线,已知此线过圆上某点,连接圆心与这点(即为半径),再证垂直即可.

练习册系列答案
相关题目
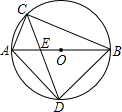 (2013•梧州一模)已知在⊙O中,直径AB为10cm,弦AC为6cm,∠ACB的平分线交⊙O于D,交AB于E,则CD的长是
(2013•梧州一模)已知在⊙O中,直径AB为10cm,弦AC为6cm,∠ACB的平分线交⊙O于D,交AB于E,则CD的长是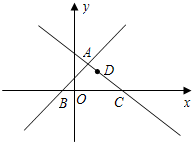 (2013•梧州一模)如图,在平面直角坐标系xOy中,直线y=x+1与y=-
(2013•梧州一模)如图,在平面直角坐标系xOy中,直线y=x+1与y=- (2013•梧州一模)如图,在3×3的正方形网格中,每个小正方形的边长为1,A、B两点在网格格点上,若C点也在网格格点上,以A、B、C三点为顶点的三角形的面积为1,则满足条件的点C的个数是( )
(2013•梧州一模)如图,在3×3的正方形网格中,每个小正方形的边长为1,A、B两点在网格格点上,若C点也在网格格点上,以A、B、C三点为顶点的三角形的面积为1,则满足条件的点C的个数是( )