题目内容
8.是否存在素数p,使得方程x2-4p(x-p)-5p-1=0的两根均为整数?若存在,求出p的所有可能值及方程的根;若不存在,请说明理由.分析 将原方程变现为一般式,根据方程有两个整数根即可得出△=4×(5p+1)为完全平方数,设5p+1=n2,根据5p=n2-1=(n-1)(n+1),即可得出n-1、n+1中至少有一个是5的倍数,即n=5k±1(k为正整数),结合p为素数即可求出p、k的值,将p的值代入原方程,再解方程即可得出结论.
解答 解:原方程可变形为x2-4px+4p2-5p-1=0,
∵方程的两根均为整数,
∴△=(-4p)2-4×(4p2-5p-1)=4×(5p+1)为完全平方数,
∴5p+1为完全平方数.
设5p+1=n2,
∵p为素数,
∴p≥2,
∴n≥4,且n为整数.
∵5p=n2-1=(n-1)(n+1),
∴n-1、n+1中至少有一个是5的倍数,即n=5k±1(k为正整数),
∴5p+1=25k2±10k+1,
∴p=k(5k±2).
∵p为素数,5k±2>1,
∴k=1,p=3或7.
当p=3时,原方程为x2-12x+20=0,
解得:x1=2,x2=10;
当p=7时,原方程为x2-28x+160=0
解得:x1=8,x2=20.
点评 本题考查了根的判别式以及解一元二次方程,根据方程有两个整数根得出△=4×(5p+1)为完全平方数是解题的关键.

练习册系列答案
相关题目
18.在运用有理数加法法则求两个有理数的和时,下列的一些思考步骤中最先进行的是( )
| A. | 求两个有理数的绝对值,并比较大小 | |
| B. | 确定和的符号 | |
| C. | 观察两个有理数的符号,并作出一些判断 | |
| D. | 用较大的绝对值减去较小的绝对值 |
13.已知x<y,下列不等式成立的有( )
①x-3<y-3;②2x<2y;③-5x<-5y;④-4x+2<-4y+2.
①x-3<y-3;②2x<2y;③-5x<-5y;④-4x+2<-4y+2.
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
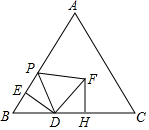 如图,在等边△ABC中,AB=10,BD=4,BE=2,点P从点E出发沿EA方向运动,连接PD,以PD为边,在PD右侧按如图方式作等边△DPF.
如图,在等边△ABC中,AB=10,BD=4,BE=2,点P从点E出发沿EA方向运动,连接PD,以PD为边,在PD右侧按如图方式作等边△DPF.