题目内容
如图,点P在⊙O的直径BA的延长线上,AB=2PA,PC切⊙O于点C,连接BC.(1)求∠P的正弦值;
(2)若⊙O的半径r=2cm,求BC的长度.

【答案】分析:(1)连接OC,则PC⊥OC,又AB=2PA,则有OC=AO=AP= PO,于是∠P=30°,可证sin∠P=
PO,于是∠P=30°,可证sin∠P= ;
;
(2)连接AC,证得△CAO是正三角形,那么CA=r=2,再根据勾股定理可求得CB的长.
解答: 解:(1)连接OC,
解:(1)连接OC,
∵PC切⊙O于点C,
∴PC⊥OC
又∵AB=2PA
∴OC=AO=AP= PO
PO
∴∠P=30°
∴sin∠P= ;
;
(或:在Rt△POC,sin∠P= )
)
(2)连接AC,
∵AB是直径,
∴∠ACB=90°,
∵∠COA=90°-30°=60°,
又∵OC=OA,
∴△CAO是正三角形.
∴CA=r=2,
∴CB= .
.
点评:此题综合考查了切线的性质、三角函数的定义、勾股定理等知识点.
 PO,于是∠P=30°,可证sin∠P=
PO,于是∠P=30°,可证sin∠P= ;
;(2)连接AC,证得△CAO是正三角形,那么CA=r=2,再根据勾股定理可求得CB的长.
解答:
 解:(1)连接OC,
解:(1)连接OC,∵PC切⊙O于点C,
∴PC⊥OC
又∵AB=2PA
∴OC=AO=AP=
 PO
PO∴∠P=30°
∴sin∠P=
 ;
;(或:在Rt△POC,sin∠P=
 )
)(2)连接AC,
∵AB是直径,
∴∠ACB=90°,
∵∠COA=90°-30°=60°,
又∵OC=OA,
∴△CAO是正三角形.
∴CA=r=2,
∴CB=
 .
.点评:此题综合考查了切线的性质、三角函数的定义、勾股定理等知识点.

练习册系列答案
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案
相关题目
 28、如图所示,在直角坐标系中,矩形OBCD的边长OB=4,OD=2.
28、如图所示,在直角坐标系中,矩形OBCD的边长OB=4,OD=2.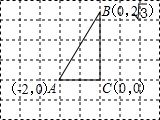 BC的2倍,“宝藏”就在矩形未知的顶点处,那么“宝藏”的位置可能是
BC的2倍,“宝藏”就在矩形未知的顶点处,那么“宝藏”的位置可能是 OB方向运动,运动速度是1个单位/秒,运动时间为t秒,直到点P与点B重合为止.
OB方向运动,运动速度是1个单位/秒,运动时间为t秒,直到点P与点B重合为止. (2013•龙湾区一模)如图,热气球从山顶A竖直上升至点B需25秒,点D在地面上,DC⊥AB,垂足为C,从地面上点D分别仰视A,B两点,测得∠ADC=20°,∠BDC=60°,若CD=130米.求该热气球从山顶A竖直上升至点B的平均速度.(结果精确到0.1米/秒)
(2013•龙湾区一模)如图,热气球从山顶A竖直上升至点B需25秒,点D在地面上,DC⊥AB,垂足为C,从地面上点D分别仰视A,B两点,测得∠ADC=20°,∠BDC=60°,若CD=130米.求该热气球从山顶A竖直上升至点B的平均速度.(结果精确到0.1米/秒)