题目内容
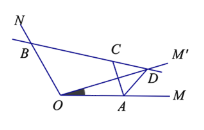
【题目】在△ABC中,AB=AC,将线段AC绕着点C逆时针旋转得到线段CD,旋转角为α.
(1)如图,∠BAC=90°,α=45°,试求点D到边AB,AC的距离的比值;
(2)如图,∠BAC=100°,α=20°,连接AD,BD,求∠CBD的大小.
【答案】(1)![]() ;(2)30°
;(2)30°
【解析】
(1)先找出点D的位置,求出△BDF∽△CDE,得出比例式,再解直角三角形求出即可;
(2)在BC上截取CF=AD,连接DF,求出△DCF≌△BAD,根据全等三角形的性质得出∠ABD=∠CDF,BD=DF,再求出答案即可.
(1)如图1,
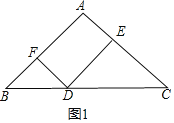
∵∠BAC=90°,AB=AC,
∴∠B=∠C=45°,
∵α=45°,
∴点D恰好落在BC上,
过点D作DE⊥AB,DF⊥AC,垂足分别为点E,F,则有:∠BED=∠DFC=90°,
∴△BDF∽△CDE,
∴![]() =
=![]() ,
,
设AB=AC=m,则有:![]() ,
,![]() ,
,
∴![]() =
=![]() =
=![]() =
=![]() -1,
-1,
即点D到边AB,AC的距离的比值为![]() ;
;
(2)如图2,在BC边上截取CF=AD,连接DF,
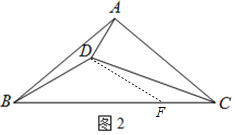
∵∠BAC=100°,AB=AC,
∴∠ABC=∠BCA=40°,
∵∠ACD=α=20°,
∴∠DCB=20°,
又∵AC=DC,
∴∠CAD=80°,
∴∠BAD=∠DCB=20°,
在△DCF和△BAD中
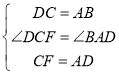
∴△DCF≌△BAD(SAS),
∴∠ABD=∠CDF,BD=DF,
∴∠DBC=∠DFB,
∵∠DBC=∠ABC-∠ABD=40°-∠ABD,∠DFB=∠DCF+∠CDF=20°+∠CDF,
∴20°+∠CDF=40°-∠ABD,
∴2∠ABD=40°-20°,
即∠ABD=10°,
∴∠CBD=∠ABC-∠ABD=40°-10°=30°.

 口算小状元口算速算天天练系列答案
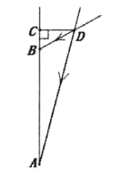
口算小状元口算速算天天练系列答案【题目】九年级某数学小组在学完《直角三角形的边角关系》这章后,决定用所学的知识设计遮阳篷(要求:遮阳篷既能最大限度地遮挡夏天炎热的阳光,又能最大限度地使冬天温暖的阳光射入室内).他们制定了设计方案,并利用课余时间完成了调查和实地测量.调查和测量项目及结果如下表:
项目 | 内容 | |
课题 | 设计遮阳篷 | |
测量示意图 |
| 如图,设计了垂直于墙面AC的遮阳篷CD,AB表示窗户的高度.榆次区一年中,夏至这一天的正午时刻,太阳光线DA与遮阳篷CD的夹角∠ADC最大;冬至这一天的正午时刻,太阳光线DB与遮阳篷CD的夹角∠CDB最小. |
调查数据 |
|
|
测量数据 |
| |
… | … | |
根据上述方案及数据,求遮阳篷![]() 的长.
的长.
(结果精确到![]() ,参考数据:
,参考数据:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() )
)