题目内容
如图,点A,B,M的坐标分别为(1, 4)、(4, 4)和(-1,0),抛物线 的顶点在线段AB(包括线段端点)上,与x轴交于C、D两点,点C在线段OM上(包括线段端点),则点D的横坐标m的取值范围是 ▲ .
的顶点在线段AB(包括线段端点)上,与x轴交于C、D两点,点C在线段OM上(包括线段端点),则点D的横坐标m的取值范围是 ▲ .
p;【答案】2≤m≤9解析:
设抛物线的解析式为:y=a(x-m)2+n,y=a(x-m)2+n的顶点在线段AB的A点上且过点O时,点D的横坐标最小,把A(1,4)代入得:y=a(x-1)2+4,把O(0,0)代入得:0=a+4,解得:a=-4,即:y=-4(x-1)2+4,由0=-(x-1)2+4得:x1=0,x2=2,
∴点D的横坐标最小值是2,当抛物线的顶点在B点,且过点M时,点D的横坐标最大,把B(4,4)y=a(x-4)2+4,把M(-1,0)代入得0=a(-1-4)2+4,解得:a=- ,即: y=-
,即: y=- (x-4)2+4,由0=-
(x-4)2+4,由0=- (x-4)2+4得:x1=9,x2=-1,∴点D的横坐标最大值是9,
(x-4)2+4得:x1=9,x2=-1,∴点D的横坐标最大值是9,
∴点D的横坐标m的取值范围是 2≤x≤9.故答案为:2≤x≤9.
设抛物线的解析式为:y=a(x-m)2+n,y=a(x-m)2+n的顶点在线段AB的A点上且过点O时,点D的横坐标最小,把A(1,4)代入得:y=a(x-1)2+4,把O(0,0)代入得:0=a+4,解得:a=-4,即:y=-4(x-1)2+4,由0=-(x-1)2+4得:x1=0,x2=2,
∴点D的横坐标最小值是2,当抛物线的顶点在B点,且过点M时,点D的横坐标最大,把B(4,4)y=a(x-4)2+4,把M(-1,0)代入得0=a(-1-4)2+4,解得:a=-
 ,即: y=-
,即: y=- (x-4)2+4,由0=-
(x-4)2+4,由0=- (x-4)2+4得:x1=9,x2=-1,∴点D的横坐标最大值是9,
(x-4)2+4得:x1=9,x2=-1,∴点D的横坐标最大值是9,∴点D的横坐标m的取值范围是 2≤x≤9.故答案为:2≤x≤9.

练习册系列答案
相关题目
 6、如图,点A,B,C的坐标分别为(2,4),(5,2),(3,-1).若以点A,B,C,D为顶点的四边形既是轴对称图形,又是中心对称图形,则点D的坐标为( )
6、如图,点A,B,C的坐标分别为(2,4),(5,2),(3,-1).若以点A,B,C,D为顶点的四边形既是轴对称图形,又是中心对称图形,则点D的坐标为( ) 29、如图,点D、E在△ABC的BC边上,∠BAD=∠CAE,要推理得出△ABE≌△ACD,可以补充的一个条件是
29、如图,点D、E在△ABC的BC边上,∠BAD=∠CAE,要推理得出△ABE≌△ACD,可以补充的一个条件是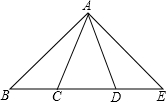 如图,点C、D在△ABE的边BE上,且AB=AE,AC=AD,求证:BC=DE.
如图,点C、D在△ABE的边BE上,且AB=AE,AC=AD,求证:BC=DE.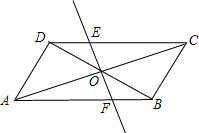 于点E、F.
于点E、F. 如图,点P为等边△ABC的边AB上一点,Q为BC延长线上一点,AP=CQ,PQ交AC于D,
如图,点P为等边△ABC的边AB上一点,Q为BC延长线上一点,AP=CQ,PQ交AC于D,