题目内容
 已知:正方形ABCD中,E、F分别是边CD、DA上的点,且CE=DF,AE与BF交于点M.
已知:正方形ABCD中,E、F分别是边CD、DA上的点,且CE=DF,AE与BF交于点M. (1)求证:△ABF≌△DAE;
(2)求证:△AMF∽△ADE;
(3)观察判断BF与AE有怎样的位置关系?
分析:(1)由四边形ABCD是正方形,易证得∠BAF=∠D=90°,AB=CD=AD,又由CE=DF,可得AF=DE,利用SAS即可判定△ABF≌△DAE;
(2)由(1),可得∠AFM=∠AED,又由∠DAE是公共角,即可判定△AMF∽△ADE;
(3)由相似三角形的对应角相等,即可得∠AMF=∠D=90°,则可得BF⊥AE.
(2)由(1),可得∠AFM=∠AED,又由∠DAE是公共角,即可判定△AMF∽△ADE;
(3)由相似三角形的对应角相等,即可得∠AMF=∠D=90°,则可得BF⊥AE.
解答:(1)证明:∵四边形ABCD是正方形,
∴∠BAF=∠D=90°,AB=CD=AD,
∵CE=DF,
∴AF=DE,
在△ABF和△DAE中,
,
∴△ABF≌△DAE(SAS);
(2)∵△ABF≌△DAE,
∴∠AFM=∠AED,
∵∠MAF=∠DAE,
∴△AMF∽△ADE;
(3)BF⊥AE.
理由:∵△AMF∽△ADE,
∴∠AMF=∠D=90°,
∴BF⊥AE.
∴∠BAF=∠D=90°,AB=CD=AD,
∵CE=DF,
∴AF=DE,
在△ABF和△DAE中,
|
∴△ABF≌△DAE(SAS);
(2)∵△ABF≌△DAE,
∴∠AFM=∠AED,
∵∠MAF=∠DAE,
∴△AMF∽△ADE;
(3)BF⊥AE.
理由:∵△AMF∽△ADE,
∴∠AMF=∠D=90°,
∴BF⊥AE.
点评:此题考查了相似三角形的判定与性质、全等三角形的判定与性质以及正方形的性质.此题难度不大,注意掌握数形结合思想的应用.

练习册系列答案
 鹰派教辅衔接教材河北教育出版社系列答案
鹰派教辅衔接教材河北教育出版社系列答案 初中暑期衔接系列答案
初中暑期衔接系列答案
相关题目
 如图,已知:正方形ABCD边长为1,E、F、G、H分别为各边上的点,且AE=BF=CG=DH,设小正方形EFGH的面积为s,AE为x,则s关于x的函数图象大致是( )
如图,已知:正方形ABCD边长为1,E、F、G、H分别为各边上的点,且AE=BF=CG=DH,设小正方形EFGH的面积为s,AE为x,则s关于x的函数图象大致是( )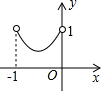
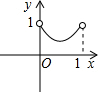
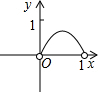
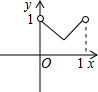
 由.
由. s的速度运动,同时动点Q在线段FC上从F?C以1cm/s的速度运动,动点G在PC上,且∠EGC=∠EQC,连接PD.设运动时间为t秒.
s的速度运动,同时动点Q在线段FC上从F?C以1cm/s的速度运动,动点G在PC上,且∠EGC=∠EQC,连接PD.设运动时间为t秒. 18、如图,已知在正方形ABCD中,P是BC上的一点,且AP=DP.求证:P是BC中点.
18、如图,已知在正方形ABCD中,P是BC上的一点,且AP=DP.求证:P是BC中点. 如图,已知在正方形ABCD外取一点E,连接AE、BE、DE.过点A作AE的垂线交DE于点P.若AE=AP=1,PB=
如图,已知在正方形ABCD外取一点E,连接AE、BE、DE.过点A作AE的垂线交DE于点P.若AE=AP=1,PB=