题目内容
先阅读材料,再根据要求回答问题
32-12=(3+1)×(3-1)=4×2
52-33=(5+3)(5-3)=8×2
72-52=(7+5)×(7-5)=12×2
(1)根据上面规律,计算
92-72=
112-92=
(2)如果用n表示正整数,请用n表示上述规律;
(3)根据这个规律,请说明连续奇数的平方差一定是8的倍数.
32-12=(3+1)×(3-1)=4×2
52-33=(5+3)(5-3)=8×2
72-52=(7+5)×(7-5)=12×2
(1)根据上面规律,计算
92-72=
(9+7)×(9-7)
(9+7)×(9-7)
=16×2
16×2
.112-92=
(11+9)×(11-9)
(11+9)×(11-9)
=20×2
20×2
.(2)如果用n表示正整数,请用n表示上述规律;
(3)根据这个规律,请说明连续奇数的平方差一定是8的倍数.
分析:(1)根据平方差公式求出即可;
(2)根据已知算式得出(2n+1)2-(2n-1)2=[(2n+1)+(2n-1)]×[(2n+1)-(2n-1)]=4n×2;
(3)设两个连续奇数是2n+1和2n-1(n为整数),得出(2n+1)2-(2n-1)2=4n×2=8n,即可得出答案.
(2)根据已知算式得出(2n+1)2-(2n-1)2=[(2n+1)+(2n-1)]×[(2n+1)-(2n-1)]=4n×2;
(3)设两个连续奇数是2n+1和2n-1(n为整数),得出(2n+1)2-(2n-1)2=4n×2=8n,即可得出答案.
解答:解:(1)92-72=(9+7)×(9-7)=16×2;
112-92=(11+9)×(11-9)=20×2.
故答案为:(9+7)×(9-7),16×2,(11+9)×(11-9),20×2;
(2)(2n+1)2-(2n-1)2
=[(2n+1)+(2n-1)]×[(2n+1)-(2n-1)]
=4n×2;
(3)设两个连续奇数是2n+1和2n-1(n为整数),
则(2n+1)2-(2n-1)2
=[(2n+1)+(2n-1)]×[(2n+1)-(2n-1)]
=4n×2
=8n;
即连续奇数的平方差一定是8的倍数.
112-92=(11+9)×(11-9)=20×2.
故答案为:(9+7)×(9-7),16×2,(11+9)×(11-9),20×2;
(2)(2n+1)2-(2n-1)2
=[(2n+1)+(2n-1)]×[(2n+1)-(2n-1)]
=4n×2;
(3)设两个连续奇数是2n+1和2n-1(n为整数),
则(2n+1)2-(2n-1)2
=[(2n+1)+(2n-1)]×[(2n+1)-(2n-1)]
=4n×2
=8n;
即连续奇数的平方差一定是8的倍数.
点评:本题考查了平方差公式,有理数的混合运算等知识点,能根据已知算式得出规律是解此题的关键.

练习册系列答案
相关题目
 的值,我们可以按照如下方法进行:
的值,我们可以按照如下方法进行:  = 2S ②
= 2S ② = S ∴
= S ∴  = S
= S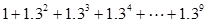 = 。
= 。 元。⑵若2年后归还本息,则要还
元。⑵若2年后归还本息,则要还 元。⑶若3年后归还本息,则要还
元。⑶若3年后归还本息,则要还 元。 )
元。 ) 的值,我们可以按照如下方法进行:
的值,我们可以按照如下方法进行:  =
2S ②
=
2S ②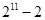 = S ∴
= S ∴  =
S
=
S = 。
= 。 元。⑵若2年后归还本息,则要还
元。⑵若2年后归还本息,则要还 元。⑶若3年后归还本息,则要还
元。⑶若3年后归还本息,则要还 元。
)
元。
)