题目内容
如图,已知抛物线![]() 与x轴相交于A、B两点,与y轴相交于点C,若已知A点坐标为A(-2, 0).
与x轴相交于A、B两点,与y轴相交于点C,若已知A点坐标为A(-2, 0).
(1)求抛物线的解析式及它的对称轴方程;
(2)求C点坐标,连接AC、BC并求线段BC所在直线的解析式;
(3)试判断△AOC与△COB是否相似?并说明理由;
(4)在抛物线的对称轴上是否存在点Q,使△ACQ为等腰三角形,若存在,求出符合条件的Q点坐标;若不存在,请说明理由.

解:(1)∵抛物线![]() 的图象经过点A(-2, 0)
的图象经过点A(-2, 0)
![]() ∴有
∴有![]() ………………………1分
………………………1分
∴![]()
∴ ![]() ………………………………………………2分
………………………………………………2分
∴ 抛物线解析式为![]() ……………3分
……………3分
∴对称轴方程为:
即![]() 为所求……………
为所求……………![]()
![]() …………………………4分
…………………………4分
(或用配方法求出对称轴方程,酌情给分)
(2)在![]() 中,令
中,令![]() 则
则
![]()
∴ 点C(0, 4) ……………………………………………1分
令![]() ,则
,则![]() ………………………2分
………………………2分
![]()
![]() …………………………………………3分
…………………………………………3分
∴ A(-2, 0) B(8, 0) …………………………………4分
设直线BC的解析式为![]() ,
,
把![]() B(8, 0), C(0, 4)的坐标分别代入解析式
B(8, 0), C(0, 4)的坐标分别代入解析式
则有,![]() ……………………………………5分
……………………………………5分
∴ 
∴ 直线BC的解析式为![]() …………………6分
…………………6分
(3)可判定△AOC∽△COB成立.…………………………1分
理由如下:在△AOC与△COB中
∵OA=2 ,OC=4 ,OB=8
∴![]()
![]() ………………………2分
………………………2分
∴有,![]() ………………………………………3分
………………………………………3分
又![]() ∠AOC=∠BOC=90°…………………………………4分
∠AOC=∠BOC=90°…………………………………4分
∴△AOC∽△COB………………………………………5分
(4)∵抛物线的对称轴方程为:![]()
可设点Q(3, t)则可求得,
![]()
![]()
![]() ………1分
………1分
i)当![]() 时,
时,
有![]()
![]()
![]()
![]() ∴ Q1(3, 0) …………………2分
∴ Q1(3, 0) …………………2分
ii)当![]() 时,
时,
有![]()
![]() ,此时方程无实数根.
,此时方程无实数根.
∴ 此时△ACQ不能构成等腰三角形……3分
iii)当![]() 时,
时,
![]()
![]()
![]()
∴ 点Q坐标为:Q2(3, ![]() ) Q3(3,
) Q3(3, ![]() )…………………5分
)…………………5分
故满足条件的Q点坐标为:Q1(3, 0), Q2(3, ![]() ) , Q3(3,
) , Q3(3, ![]() )
)


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案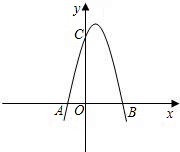 如图,已知抛物线与x轴交于点A(-2,0),B(4,0),与y轴交于点C(0,8).
如图,已知抛物线与x轴交于点A(-2,0),B(4,0),与y轴交于点C(0,8).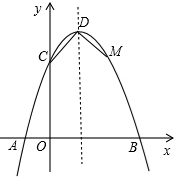 如图,已知抛物线与x轴交于点A(-1,0),与y轴交于点C(0,3),且对称轴方程为x=1
如图,已知抛物线与x轴交于点A(-1,0),与y轴交于点C(0,3),且对称轴方程为x=1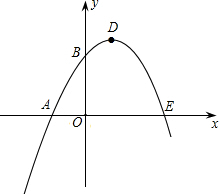 函数的最大值是4.
函数的最大值是4. (2012•株洲)如图,已知抛物线与x轴的一个交点A(1,0),对称轴是x=-1,则该抛物线与x轴的另一交点坐标是( )
(2012•株洲)如图,已知抛物线与x轴的一个交点A(1,0),对称轴是x=-1,则该抛物线与x轴的另一交点坐标是( )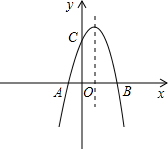 如图,已知抛物线与x轴交于点A(-2,0),B(4,0),与y轴交于点C(0,8).
如图,已知抛物线与x轴交于点A(-2,0),B(4,0),与y轴交于点C(0,8).