题目内容
如图,AB是⊙O的直径,∠A=![]() ,延长OB到D,使BD=OB.
,延长OB到D,使BD=OB.
(1)△OCB是否是等边三角形?说明你的理由;
(2)求证:DC是⊙O的切线.


(1)解法一:∵∠A=![]() ,∴∠COB=
,∴∠COB=![]() .
.
又OC=OB, ∴△OCB是等边三角形.
解法二:∵AB是⊙O的直径,∴∠ACB=![]() .
.
又∵∠A=![]() , ∴∠ABC=
, ∴∠ABC=![]() .
.
又OC=OB, ∴△OCB是等边三角形.
(2)证明:由(1)知:BC=OB,∠OCB=∠OBC=![]() .
.
又∵BD=OB,∴BC=BD.
∴∠BCD=∠BDC=![]() ∠OBC=
∠OBC=![]() .
.
∴∠OCD=∠OCB+∠BCD=![]() ,故DC是⊙O的切线.
,故DC是⊙O的切线.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目



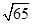 B.3
B.3 C.8 D.2
C.8 D.2