题目内容
【题目】如图，在Rt△ABC中，∠ABC=90° ，∠ACB=30° ，AD平分∠BAC， BD= 
，点P为线段AC上的一个动点
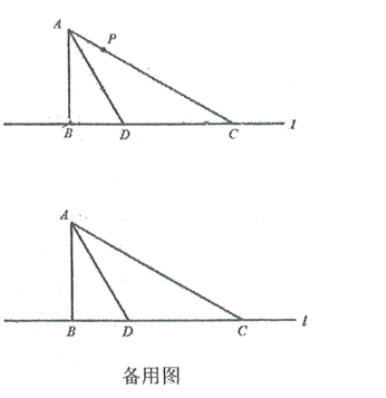
(1)求AC的长
(2)作△ABC中∠ACB的角平分线CH，求BH的长
(3)若点E在直线1上，且在C点的左侧，PE=PC， AP为多少时，△ACE为等腰三角形?
【答案】（1）6；（2）
；（3）
或0或4.
【解析】
（1）易得∠BAD=30°，∴AD=2BD，再由勾股定理求出AB，最后再由30°的直角边是斜边的一半可得AC=2AB.
（2）过H点作HG⊥AC于点G，设BH=x，在Rt△AHG中用勾股定理建立方程求解；
（3）分三种情况讨论：①AC=EC，②AC=AE，③AE=EC，分别根据题意找出P点的位置，采用（2）的方法建立方程求解.
解：（1）∵∠ABC=90° ，∠ACB=30°
∴∠BAC=60°，
又∵AD平分∠BAC
∴∠BAD=30°，
在Rt△ABD中，BD= 
∴AD=2BD=
在Rt△ABC中，∠ACB=30°，∴AC=2AB=6
（2）如图所示，过H点作HG⊥AC于点G，
在Rt△ABC中，
∵CH平分∠BCA，∴∠HCB=∠HCG
在△HCB和△HCG中
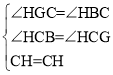
∴△HCB≌△HCG（AAS）
∴BH=HG，CG=BC
设BH=x，则HG=x，AH=3-x，AG=
在Rt△AHG中，
AG+HG=AH，即
解得
∴BH的长为
（3）△ACE为等腰三角形，①若AC=EC，如图所示，由PE=PC可知P点在EC的中垂线上，则作EC的中垂线与AC的交点即为P点，
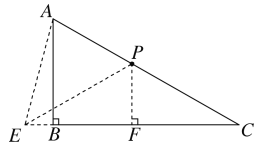
∵PF为EC的中垂线，∴FC=
，
在Rt△PCF中，∵∠C=30°，∴PC=2PF
设PF=a，则PC=2a，
有勾股定理得
，解得
∴PC=
，∴
②若AC=AE，如图所示，此时P点与A重合，∴AP=0
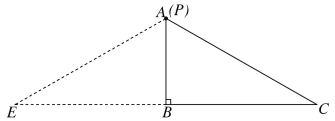
③若AE=EC，如图所示，由PE=PC可知P点在CE的中垂线上，所以作EC的中垂线与AC的交点即为P点，
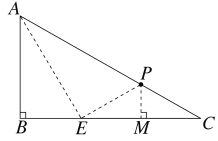
设AE=EC=x，则BE=
在Rt△ABE中，由勾股定理得，
，解得
∴EC=
又∵PM垂直平分EC，∴MC=
在Rt△PMC中，∠C=30°，
设PM=y，则PC=2y，由勾股定理得
，解得
∴PC=2，此时AP=6-2=4
综上，当AP为或0或4时，△ACE为等腰三角形
